定積分の台形公式

この台形公式を使用して、定積分を解くことができます。関数f（x）を範囲aからbの間で統合することは、基本的に、点x=aからx=bまでの曲線の下の領域を見つけることです。

その領域を見つけるために、領域をn個の台形に分割でき、各台形の幅はhなので、（b --a）=nhと言うことができます。台形の数が増えると、面積計算の結果がより正確になります。積分を解くために、この公式に従います。

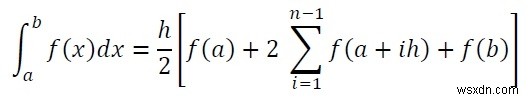
ここで、hは間隔の幅、nは間隔の数です。

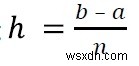
入力と出力

Input:
The function f(x): 1-exp(-x/2.0) and limits of the integration: 0, 1. The number of intervals: 20
Output:
The answer is: 0.21302

アルゴリズム

integrateTrapezoidal(a, b, n)

入力： 下限と上限、および積分の数n。

出力： 統合の結果。

Begin
   h := (b - a)/n
   sum := f(a) + f(b)
   for i := 1 to n, do
      sum := sum + f(a + ih)
   done
   return sum
End

例

#include<iostream>
#include<cmath>
using namespace std;

float mathFunc(float x) {
   return (1-exp(-x/2.0));    //the function 1 - e^(-x/2)
}

float integrate(float a, float b, int n) {
   float h, sum;
   int i;
   h = (b-a)/n;    //calculate the distance between two interval
   sum = (mathFunc(a)+mathFunc(b))/2;    //initial sum using f(a) and f(b)

   for(i = 1; i<n; i++) {
      sum += mathFunc(a+i*h);
   }
   return (h*sum);    //The result of integration
}

main() {
   float result, lowLim, upLim;
   int interval;
   cout << "Enter Lower Limit, Upper Limit and interval: "; cin >>lowLim >>upLim >>interval;
   result = integrate(lowLim, upLim, interval);
   cout << "The answer is: " << result;
}

出力

Enter Lower Limit, Upper Limit and interval: 0 1 20
The answer is: 0.21302