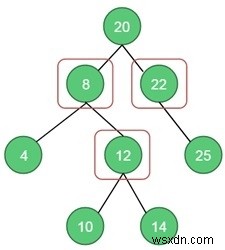
頂点被覆問題

無向グラフの場合、頂点被覆は頂点のサブセットであり、グラフのすべてのエッジ（u、v）について、uまたはvのいずれかがセットに含まれます。

二分木を使用すると、頂点被覆問題を簡単に解決できます。

この問題は、2つのサブ問題に分けることができます。ルートが頂点被覆の一部である場合。この場合、ルートはすべての子エッジをカバーします。左右のサブツリーの頂点被覆のサイズを簡単に見つけて、ルートに1を追加できます。

入力と出力

Input:
A binary tree.
Output:
The vertex cover is 3.
 

アルゴリズム

vertexCover(root node)

この問題では、1つの二分木が形成され、各ノードはそのノードがカバーする頂点のデータと数を保持します。

入力- 二分木のルート。

出力- ルートによってカバーされる頂点の数。

Begin
   if root is φ, then
      return 0
   if root has no child, then
      return 0
   if vCover(root) ≠ 0, then
      return vCover(root)
   withRoot := 1 + vertexCover(left(root)) + vertexCover(right(root))
   withoutRoot := 0

   if root has left child, then
      withoutRoot := withoutRoot + vertexCover(left(left(root))) + vertexCover(left(right(root)))
   if root has right child, then
      withoutRoot := withoutRoot + vertexCover(right(left(root))) + vertexCover(right(right(root)))
   return vCover(root)
End

例

#include <iostream>
#include <algorithm>
using namespace std;

struct node {
   int data;
   int vCover;
   node *left, *right;
};

node *getNode(int data) {
   node *newNode = new (node);
   newNode->data = data;
   newNode->vCover = 0; //set vertex cover to 0
   newNode->left = NULL;
   newNode->right = NULL;
   return newNode;    //newly created node
}

int vertexCover(node *root) {
   if(root == NULL)    //when tree is empty
      return 0;
   if(root->left == NULL && root->right == NULL)    //when no other edge from root
      return 0;
         
   if(root->vCover != 0)   //when vertex cover of this node is found, leave that node
      return root->vCover;
         
   int sizeWithRoot = 1 + vertexCover(root->left) + vertexCover(root->right);
   int sizeWithOutRoot = 0;
   
   if(root->left != NULL)   //when root is not included and go for left child
      sizeWithOutRoot += 1 + vertexCover(root->left->left) + vertexCover(root->left->right);
   if(root->right != NULL)    //when root is not included and go for right child
      sizeWithOutRoot += 1 + vertexCover(root->right->left) + vertexCover(root->right->right);
   
   root->vCover = (sizeWithRoot < sizeWithOutRoot)?sizeWithRoot:sizeWithOutRoot; //minimum vertex cover
   return root->vCover;
}

int main() {
   //create tree to check vertex cover
   node *root = getNode(20);
   root->left = getNode(8); root->right = getNode(22);
   root->left->left = getNode(4); root->left->right = getNode(12);
   root->left->right->left = getNode(10); root->left->right->right = getNode(14);
   root->right->right = getNode(25);
   cout << "Minimal vertex cover: " << vertexCover(root);
}

出力

Minimal vertex cover: 3