トポロジカルソート

有向非巡回グラフのトポロジカルソートは、頂点の線形順序付けです。有向グラフのすべてのエッジU-Vについて、頂点uは順序付けで頂点vの前に来ます。

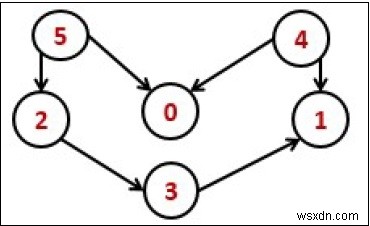
ソース頂点はデスティネーション頂点の後に来ることがわかっているので、スタックを使用して前の要素を格納する必要があります。すべてのノードが完成したら、スタックからノードを表示するだけです。

入力と出力

Input:
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
1 1 0 0 0 0
1 0 1 0 0 0

Output:
Nodes after topological sorted order: 5 4 2 3 1 0

アルゴリズム

topoSort（u、visited、stack）

入力- 開始頂点u、どのノードが訪問されたかを追跡するための配列。ノードを格納するためのスタック。
出力- スタック内のトポロジ順で頂点を並べ替えます。

Begin
   mark u as visited
   for all vertices v which is adjacent with u, do
      if v is not visited, then
         topoSort(c, visited, stack)
   done

   push u into a stack
End

PerformTopologicalSorting（Graph）

入力- 与えられた有向非巡回グラフ。
出力- ノードのシーケンス。

Begin
   initially mark all nodes as unvisited
   for all nodes v of the graph, do
      if v is not visited, then
         topoSort(i, visited, stack)
   done
   pop and print all elements from the stack
End.

例

#include<iostream>
#include<stack>
#define NODE 6
using namespace std;

int graph[NODE][NODE] = {
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 1, 0, 0},
   {0, 1, 0, 0, 0, 0},
   {1, 1, 0, 0, 0, 0},
   {1, 0, 1, 0, 0, 0}
};

void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;                //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {             //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }
   stk.push(u);     //push starting vertex into the stack
}

void performTopologicalSort() {
   stack<int> stk;
   bool vis[NODE];

   for(int i = 0; i<NODE; i++)
      vis[i] = false;     //initially all nodes are unvisited

   for(int i = 0; i<NODE; i++)
      if(!vis[i])     //when node is not visited
         topoSort(i, vis, stk);

   while(!stk.empty()) {
      cout << stk.top() << " ";
      stk.pop();
   }
}

main() {
   cout << "Nodes after topological sorted order: ";
   performTopologicalSort();
}

出力

Nodes after topological sorted order: 5 4 2 3 1 0