強く接続されたコンポーネントのためのタージャンのアルゴリズム

Tarjanのアルゴリズムは、有向グラフの強連結成分を見つけるために使用されます。このアルゴリズムを実装するために必要なDFSトラバーサルは1つだけです。

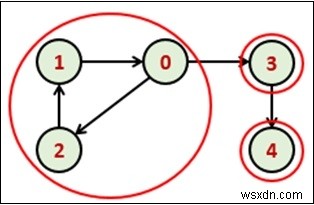
DFSトラバーサルを使用して、フォレストのDFSツリーを見つけることができます。 DFSツリーから、強く接続されたコンポーネントが見つかります。そのようなサブツリーのルートが見つかると、サブツリー全体を表示できます。そのサブツリーは、1つの強連結成分です。

入力と出力

Input:
Adjacency matrix of the graph.
0 0 1 1 0
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
0 0 0 0 0

Output:
The strongly connected components:
4
3
1 2 0

アルゴリズム

findComponent（u、disc、low、stack、stackItemFlag）

入力： 開始ノード、検出時間、低、ディスクは頂点の検出時間を保持し、低はサブツリーに関する情報を保持します。頂点を保持するスタックと、スタック内のノードを追跡する別のフラグ配列。

出力： SCCを表示します。

Begin
   time := 0      //the value of time will not be initialized for next function calls
   set disc[u] := time+1 and low[u] := time + 1
   time := time + 1
   push u into stack
   stackItemFalg[u] := true

   for all vertex v which is adjacent with u, do
      if v is not discovered, then
         fincComponent(v, disc, low, stack, stackItemFalg)
         low[u] = minimum of low[u] and low[v]
      else if stackItemFalg[v] is true, then
         low[u] := minimum of low[u] and disc[v]
   done

   poppedItem := 0
   if low[u] = disc[u], then
      while u is not in the stack top, do
         poppedItem := top of stack
         display poppedItem
         stackItemFlag[poppedItem] := false
         pop item from stack
      done

      poppedItem := top of stack
      display poppedItem
      stackItemFlag[poppedItem] := false
      pop item from stack
End

strongConComponent（graph）

入力＆、マイナス; 与えられたグラフ。

出力- 強く接続されたすべてのコンポーネント。

Begin
   initially set all items in the disc array to undiscovered
   for all elements in low to φ
   and mark no item is stored into the stack

   for all node i in the graph, do
      if disc[i] is undiscovered, then
         findComponent(i, disc, low, stack, stackItemFlag)
End

例

#include<iostream>
#include<stack>
#define NODE 5
using namespace std;
                               
int graph[NODE][NODE] = {
   {0, 0, 1, 1, 0},
   {1, 0, 0, 0, 0},
   {0, 1, 0, 0, 0},
   {0, 0, 0, 0, 1},
   {0, 0, 0, 0, 0}
};
                               
int min(int a, int b) {
   return (a<b)?a:b;
}
                               
void findComponent(int u, int disc[], int low[], stack<int>&stk, bool stkItem[]) {
   static int time = 0;
   disc[u] = low[u] = ++time;    //inilially discovery time and low value is 1
   stk.push(u);
   stkItem[u] = true;    //flag as u in the stack
   
   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {
         if(disc[v] == -1) {   //when v is not visited
            findComponent(v, disc, low, stk, stkItem);
            low[u] = min(low[u], low[v]);
         } else if(stkItem[v])    //when v is in the stack, update low for u
            low[u] = min(low[u], disc[v]);
      }
   }
   
   int poppedItem = 0;
   if(low[u] == disc[u]) {
      while(stk.top() != u) {
         poppedItem = stk.top();
         cout << poppedItem << " ";
         stkItem[poppedItem] = false;    //mark as item is popped
         stk.pop();
      }
      poppedItem = stk.top();
      cout << poppedItem <<endl;
      stkItem[poppedItem] = false;
      stk.pop();
   }
}
                               
void strongConComponent() {
   int disc[NODE], low[NODE];
   bool stkItem[NODE];
   stack<int> stk;
   
   for(int i = 0; i<NODE; i++) {    //initialize all elements
      disc[i] = low[i] = -1;
      stkItem[i] = false;
   }
   
   for(int i = 0; i<NODE; i++)    //initialize all elements
      if(disc[i] == -1)
         findComponent(i, disc, low, stk, stkItem);
}

int main() {
   strongConComponent();
}

出力

4
3
1 2 0