有向グラフでサイクルを検出する

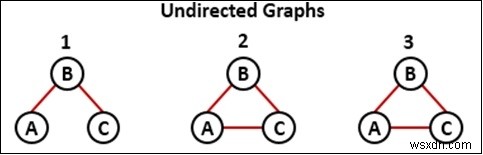
深さ優先探索（DFS）トラバーサルアルゴリズムを使用して、有向グラフでサイクルを検出できます。いずれかのノードに自己ループがある場合、それはサイクルと見なされます。そうでない場合、子ノードに親を接続するための別のエッジがある場合、それもサイクルになります。

切断されたグラフの場合、異なる木が存在する可能性があり、それらを森と呼ぶことができます。次に、森のすべての木の周期を検出する必要があります。

このアプローチでは、さまざまなセットを使用して、DFSトラバーサルを実行するノードを割り当てます。ホワイト、グレー、ブラックの3つのセットがあります。最初は、すべてのノードがホワイトセット内に保存されます。 1つの新しいノードがトラバースされると、それは灰色のセットに格納され、白いノードから削除されます。そして、バックトラックを完了した後、そのノードのタスクが完了すると、灰色から黒色のセットに交換されます。

入力と出力

Input:
The Adjacency matrix.

0 1 0 0 0
0 0 0 0 0
1 0 0 1 0
0 0 0 0 1
0 0 1 0 0

Output:
The graph has cycle. 

アルゴリズム

dfs（curr、wSet、gSet、bSet）

入力： 現在のノード、白、灰色、黒のセット。

出力： サイクルがある場合は真。

Begin
   delete curr from the while set and add it to the grey set
   for all nodes v connected with curr in the graph, do
      if v is in the black set, then
         skip next part, and go for next iteration
      if v is in the grey set, then
         return true
      if dfs(v, wSet, gSet, bSet) is true, then
         return true
   done
   delete curr from grey set and add to black set
   return fasle
End

hasCycle（グラフ）

入力- 与えられたグラフ。

出力： グラフが循環している場合はTrue。

Begin
   initially insert all nodes into the white set
   while white set has some elements, do
      for all nodes v in the graph, do
         if v is not in the white set, then
            if dfs(v, wSet, gSet, bSet), then
               return true
      done
   done
   return false
End

例

#include<iostream>
#include<set>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 1, 0, 0, 0},
   {0, 0, 0, 0, 0},
   {1, 0, 0, 1, 0},
   {0, 0, 0, 0, 1},
   {0, 0, 1, 0, 0}
};

bool dfs(int curr, set<int>&wSet, set<int>&gSet, set<int>&bSet) {
   //moving curr to white set to grey set.
   wSet.erase(wSet.find(curr));
   gSet.insert(curr);

   for(int v = 0; v < NODE; v++) {
      if(graph[curr][v] != 0) {    //for all neighbour vertices
         if(bSet.find(v) != bSet.end())
            continue;    //if the vertices are in the black set
         if(gSet.find(v) != gSet.end())
            return true;    //it is a cycle
         if(dfs(v, wSet, gSet, bSet))
            return true;    //cycle found
      }
   }

   //moving v to grey set to black set.
   gSet.erase(gSet.find(curr));
   bSet.insert(curr);
   return false;
}

bool hasCycle() {
   set<int> wSet, gSet, bSet;    //three set as white, grey and black
   for(int i = 0; i<NODE; i++)
      wSet.insert(i);    //initially add all node into the white set

   while(wSet.size() > 0) {
      for(int current = 0; current < NODE; current++) {
         if(wSet.find(current) != wSet.end())
            if(dfs(current, wSet, gSet, bSet))
               return true;
      }
   }
   return false;
}

int main() {
   bool res;
   res = hasCycle();
   if(res)
      cout << "The graph has cycle." << endl;
   else
      cout << "The graph has no cycle." << endl;
}

出力

The graph has cycle.