最大二部マッチング

2部マッチングとは、グラフ内のエッジのセットが、そのセット内の2つのエッジがエンドポイントを共有しないように選択されることです。最大一致は、エッジの最大数と一致しています。

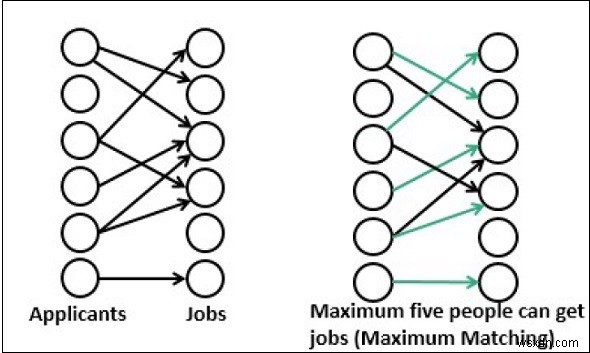
最大の一致が見つかった場合、別のエッジを追加することはできません。最大一致グラフに1つのエッジが追加されると、それは一致しなくなります。 2部グラフの場合、最大マッチングが複数存在する可能性があります。

入力と出力

Input:
The adjacency matrix.
0 1 1 0 0 0
1 0 0 1 0 0
0 0 1 0 0 0
0 0 1 1 0 0
0 0 0 0 0 0
0 0 0 0 0 1

Output:
Maximum number of applicants matching for job: 5

アルゴリズム

bipartiteMatch（u、visited、assign）

入力： ノードを開始し、リストにアクセスして追跡し、リストを割り当ててノードを別のノードに割り当てます。

出力- 頂点uのマッチングが可能な場合はtrueを返します。

Begin
   for all vertex v, which are adjacent with u, do
      if v is not visited, then
         mark v as visited
         if v is not assigned, or bipartiteMatch(assign[v], visited, assign) is true, then
            assign[v] := u
            return true
   done
   return false
End

maxMatch（グラフ）

入力- 与えられたグラフ。

出力- 試合の最大数。

Begin
   initially no vertex is assigned
   count := 0
   for all applicant u in M, do
      make all node as unvisited
      if bipartiteMatch(u, visited, assign), then
         increase count by 1
   done
End

例

#include <iostream>
#define M 6
#define N 6
using namespace std;

bool bipartiteGraph[M][N] = {    //A graph with M applicant and N jobs
   {0, 1, 1, 0, 0, 0},
   {1, 0, 0, 1, 0, 0},
   {0, 0, 1, 0, 0, 0},
   {0, 0, 1, 1, 0, 0},
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 0, 0, 1}
};

bool bipartiteMatch(int u, bool visited[], int assign[]) {
   for (int v = 0; v < N; v++) {    //for all jobs 0 to N-1
      if (bipartiteGraph[u][v] && !visited[v]) {    //when job v is not visited and u is interested
         visited[v] = true;    //mark as job v is visited
         //when v is not assigned or previously assigned
         if (assign[v] < 0 || bipartiteMatch(assign[v], visited, assign)) {
            assign[v] = u;    //assign job v to applicant u
            return true;
         }
      }
   }
   return false;
}

int maxMatch() {
   int assign[N];    //an array to track which job is assigned to which applicant
   for(int i = 0; i<N; i++)
      assign[i] = -1;    //initially set all jobs are available
   int jobCount = 0;

   for (int u = 0; u < M; u++) {    //for all applicants
      bool visited[N];
      for(int i = 0; i<N; i++)
         visited[i] = false;    //initially no jobs are visited
      if (bipartiteMatch(u, visited, assign))    //when u get a job
         jobCount++;
   }
   return jobCount;
}

int main() {
   cout << "Maximum number of applicants matching for job: " << maxMatch();
}

出力

Maximum number of applicants matching for job: 5