グラフの幅優先探索（BFS）

幅優先探索（BFS）トラバーサルはアルゴリズムであり、特定のグラフのすべてのノードにアクセスするために使用されます。このトラバーサルアルゴリズムでは、1つのノードが選択され、隣接するすべてのノードが1つずつ訪問されます。隣接するすべての頂点を完了すると、さらに移動して別の頂点をチェックし、隣接する頂点を再度チェックします。

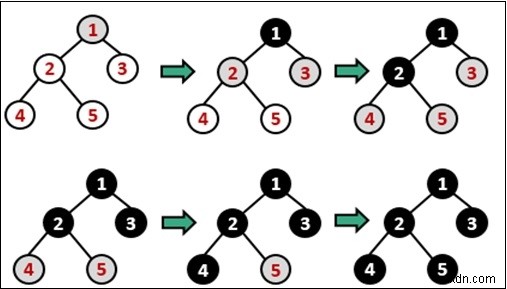
このアルゴリズムを実装するには、キューデータ構造を使用する必要があります。隣接するすべての頂点が完了すると、隣接するすべての頂点がキューに追加され、1つのアイテムがキューから削除され、その頂点を再び通過し始めます。

グラフでは、サイクルが発生することがあるため、配列を使用して、ノードがすでにアクセスされているかどうかをマークします。

入力と出力

Input:
The Adjacency matrix of the graph.

     A B C D E F
   A 0 1 1 1 0 0
   B 1 0 0 1 1 0
   C 1 0 0 1 0 1
   D 1 1 1 0 1 1
   E 0 1 0 1 0 1
   F 0 0 1 1 1 0

Output:
BFS Traversal: B A D E C F

アルゴリズム

bfs(vertices, start)

入力- 頂点のリストと開始頂点。​​

出力- グラフが接続されている場合は、すべてのノードをトラバースします。

Begin
   define an empty queue que
   at first mark all nodes status as unvisited
   add the start vertex into the que

   while que is not empty, do
      delete item from que and set to u
      display the vertex u

      for all vertices 1 adjacent with u, do
         if vertices[i] is unvisited, then
            mark vertices[i] as temporarily visited
            add v into the queue
         mark
      done

      mark u as completely visited
   done
End

例

#include<iostream>
#include<queue>
#define NODE 6
using namespace std;

typedef struct node {
   int val;
   int state;    //status
}node;

int graph[NODE][NODE] = {
   {0, 1, 1, 1, 0, 0},
   {1, 0, 0, 1, 1, 0},
   {1, 0, 0, 1, 0, 1},
   {1, 1, 1, 0, 1, 1},
   {0, 1, 0, 1, 0, 1},
   {0, 0, 1, 1, 1, 0}
};

void bfs(node *vert, node s) {
   node u;
   int i, j;
   queue<node> que;

   for(i = 0; i<NODE; i++) {
      vert[i].state = 0;    //not visited
   }

   vert[s.val].state = 1;   //visited
   que.push(s);            //insert starting node

   while(!que.empty()) {
      u = que.front();    //delete from queue and print
      que.pop();
      cout << char(u.val+'A') << " ";

      for(i = 0; i<NODE; i++) {
         if(graph[i][u.val]) {
            //when the node is non-visited
            if(vert[i].state == 0) {
               vert[i].state = 1;
               que.push(vert[i]);
            }    
         }
      }
      u.state = 2;   //completed for node u
   }
}

int main() {
   node vertices[NODE];
   node start;
   char s;

   for(int i = 0; i<NODE; i++) {
      vertices[i].val = i;
   }

   s = 'B';   //starting vertex B
   start.val = s-'A';
   cout << "BFS Traversal: ";
   bfs(vertices, start);
   cout << endl;
}

出力

BFS Traversal: B A D E C F