C++のフローネットワークで最小のs-tカットを見つける

次のフローネットワークがあるとします。ご存知のように、s-tカットは、ソースsノードとシンクtノードが異なるサブセットにある必要があるカットであり、ソースセットからシンク側に向かうエッジが含まれます。ここで、s-tカットの容量は、カットセット内の各エッジ容量の合計で表されます。ここでは、特定のネットワークの最小容量s-tカットを見つける必要があります。ここで期待される出力は、最小カットのすべてのエッジです。

したがって、入力が次のような場合

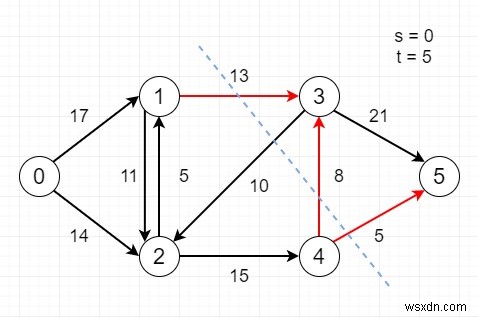
その場合、出力は[（1,3）、（4,3）、（4,5）]

これを解決するには、次の手順に従います-

• ノード=6

• 関数bfs（）を定義します。これは、graph、src、sink、array par、

  を取ります。

• サイズ-NODESの配列visを定義します。そして0で埋める

• 1つのキューキューを定義する

• srcをqueに挿入

• vis [src]：=trueおよびpar[src]：=-1

• （queは空ではありません）、実行します-

  • u1：=queの最初の要素

  • queから要素を削除

  • 初期化v1：=0の場合、v1

    • vis [v1]がfalseで、graph [u1、v1]> 0の場合、-

      • v1をqueに挿入します

      • par [v1]：=u1

      • vis [v1]：=true

• vis[sink]がtrueの場合はtrueを返します

• 関数dfs（）を定義します。これは、graph、src、array vis、

  を取ります。

• vis [src]：=true

• 初期化i：=0の場合、i

  • graph [src、i]がゼロ以外で、vis [i]がfalseの場合、-

    • dfs（graph、i、vis）

• メインの方法から、次のようにします-

• 配列temp_graphを定義し、それにグラフをコピーします

• サイズの配列パラメーターを定義します：NODES。

• bfs（temp_graph、src、sink、par）がtrueの場合、実行-

  • path_flow：=inf

  • 初期化v：=シンクの場合、vがsrcと等しくない場合は、v：=par [v]を更新し、-

    を実行します。

    • u：=par [v]

    • path_flow：=path_flowとtemp_graph[u、v]

      の最小値

  • 初期化v：=シンクの場合、vがsrcと等しくない場合は、v：=par [v]を更新し、-

    を実行します。

    • u：=par [v]

    • temp_graph [u、v]：=temp_graph [u、v] --path_flow

    • temp_graph [v、u]：=temp_graph [v、u] + path_flow

• サイズ-NODESの配列visを定義します。そしてfalseで埋める

• dfs（temp_graph、src、vis）

• 初期化i：=0の場合、i − NODESの場合、更新（iを1増やします）、実行-

• 初期化j：=0の場合、j − NODESの場合、更新（jを1増やします）、実行−

  • vis [i]がゼロ以外で、vis [j]が偽で、graph [i、j]がゼロ以外の場合、-

    • （i、j）をエッジとして表示

  • 戻る

例（C ++）

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
#define NODES 6
int bfs(int graph[NODES][NODES], int src, int sink, int par[]) {
   bool vis[NODES];
   memset(vis, 0, sizeof(vis));
   queue <int> que;
   que.push(src);
   vis[src] = true;
   par[src] = -1;
   while (!que.empty()) {
      int u1 = que.front();
      que.pop();
      for (int v1=0; v1<NODES; v1++){
         if (vis[v1]==false && graph[u1][v1] > 0) {
            que.push(v1);
            par[v1] = u1;
            vis[v1] = true;
         }
      }
   }
   return (vis[sink] == true);
}
void dfs(int graph[NODES][NODES], int src, bool vis[]) {
   vis[src] = true;
   for (int i = 0; i < NODES; i++)
   if (graph[src][i] && !vis[i])
   dfs(graph, i, vis);
}
void minCut(int graph[NODES][NODES], int src, int sink) {
   int u, v;
   int temp_graph[NODES][NODES];
   for (u = 0; u < NODES; u++)
      for (v = 0; v < NODES; v++)
         temp_graph[u][v] = graph[u][v];
   int par[NODES];
   while (bfs(temp_graph, src, sink, par)){
      int path_flow = INT_MAX;
      for (v=sink; v!=src; v=par[v]) {
         u = par[v];
         path_flow = min(path_flow, temp_graph[u][v]);
      }
      for (v=sink; v != src; v=par[v]) {
         u = par[v];
         temp_graph[u][v] -= path_flow;
         temp_graph[v][u] += path_flow;
      }
   }
   bool vis[NODES];
   memset(vis, false, sizeof(vis));
   dfs(temp_graph, src, vis);
   for (int i = 0; i < NODES; i++)
      for (int j = 0; j < NODES; j++)
         if (vis[i] && !vis[j] && graph[i][j])
            cout << "("<< i << ", " << j << ")" << endl;
   return;
}
int main() {
   int graph1[NODES][NODES] = {
      {0, 17, 14, 0, 0, 0},
      {0, 0, 11, 13, 0, 0},
      {0, 5, 0, 0, 15, 0},
      {0, 0, 9, 0, 0, 21},
      {0, 0, 0, 8, 0, 5},
      {0, 0, 0, 0, 0, 0}
   };
   minCut(graph1, 0, 5);
}

入力

{{0, 17, 14, 0, 0, 0},
{0, 0, 11, 13, 0, 0},
{0, 5, 0, 0, 15, 0},
{0, 0, 9, 0, 0, 21
{0, 0, 0, 8, 0, 5},
{0, 0, 0, 0, 0, 0}};

出力

(1, 3)
(4, 3)
(4, 5)