C++で二分木の2つのノードを結合することによって形成できる最大長サイクル

二分木が与えられます。目標は、指定されたツリーで最大の長さのサイクルを見つけることです。これを行うには、ルートノードから左側のサブツリーと右側のサブツリーの最大の高さを見つけ、これらの最大長のパスを結合して最長のサイクルを取得します。

上記のツリーの場合、最大長サイクルは1-2-3-4-7-6または1-6-7-4-3-2-1です。長さは6です。

入力 −ツリー

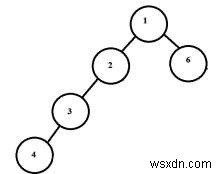
出力 −最大長サイクルは− 5

説明 −左側のサブツリーの最大高さは3、右側のサブツリーの最大高さは1です。サイクルの長さは3 + 1 + 1=5になります。サイクルは1-2-3-4-6または1-6-4-3-2

入力 −ツリー

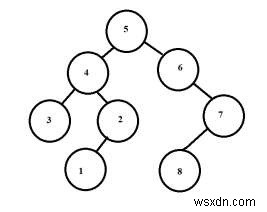
出力 −最大長サイクルは− 7

説明 −左側のサブツリーの最大高さは3で、右側のサブツリーの最大高さは3です。サイクルの長さは3 + 3 + 1=7になります。サイクルは5-4-2-1-8-7-6または5-6-7-8-1-2-4-5

以下のプログラムで使用されているアプローチは次のとおりです

• パブリックデータメンバーを持つクラスtreenodeを作成します-ノードの重みのintデータ、他のそのようなノードを指す左右のtreenodeポインター。

• 関数newNode（int data）は、データをパラメーターとして受け取り、左右のポインターをNULLとして持つノードを作成します。

• newnode（）関数を呼び出してツリーを作成します。

• 関数maxheight（treenode * root）はツリーのルートを取得し、ルートをルートとするツリーの最大高さを返します。

• この関数は、ルートがNULLであるかどうかをチェックします。つまり、高さが0であり、0を返します。

• lheightとrheightは、maxheight（root-> left）;を再帰的に呼び出すことにより、ノードルートの左右のサブツリーの高さを計算します。およびmaxheight（root-> right）;

• lheightとrheightを比較して得られた最大値を返します。

• main内に、treeNodeの左側のサブツリーと右側のサブツリーの最大の高さの値を格納します。

• これで、最大長サイクルは、ルート自体を含めたmaxlheight + maxrheight+1の合計になります。

• 結果としてサイクルの長さを印刷します。

例

#include <bits/stdc++.h>
using namespace std;
//class for tree
class treenode{
public:
   int data;
   treenode* left;
   treenode* right;
};
//find maximum height between left and right subtree of current root
int maxheight(treenode* root){
   if (root == NULL)
      return 0;
   else{
      int lheight = maxheight(root->left);
      int rheight = maxheight(root->right);
      //find maximum height
      if (lheight > rheight)
         return(lheight + 1);
      else
         return(rheight + 1);
      }
   }
   //creating a node of tree
   treenode* newNode(int data){
      treenode* Node = new treenode();
      Node->data = data;
      Node->left = NULL;
      Node->right = NULL;
      return(Node);
}
int main(){
   treenode *root = newNode(6);
   root->left = newNode(8);
   root->right = newNode(9);
   root->left->left = newNode(4);
   root->left->right = newNode(5);
   root->left->right->right = newNode(7);
   root->left->right->right->left = newNode(2);
   int maxlheight=maxheight(root->left);
   int maxrheight=maxheight(root->right);
   int maxlheight=maxDepth(root->left);
   int maxrheight=maxDepth(root->right);
   cout << "Maximum length cycle: " << maxlheight+maxrheight+1;
   return 0;
}

出力

Maximum length cycle: 6