C++での二分木の境界

二分木があるとすると、ルートから反時計回りにその境界の値を見つける必要があります。ここでの境界には、左側の境界、葉、右側の境界が含まれ、ノードが重複することはありません。

• 左側の境界は、ルートから左端のノードまでのパスです。

• 右の境界は、ルートから右端のノードまでのパスです。

• ルートに左サブツリーまたは右サブツリーがない場合、ルート自体は左境界または右境界になります。

したがって、入力が次のような場合

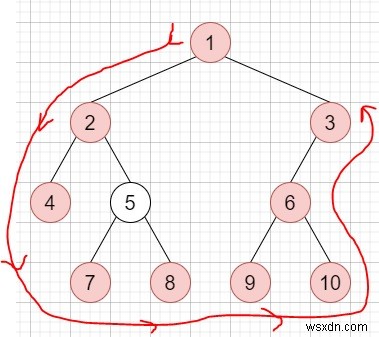
その場合、出力は[1,2,4,7,8,9,10,6,3]

これを解決するには、次の手順に従います-

• 配列retを定義する

• 関数leftBoundary（）を定義します。これはノードを取ります

• ノードがnullまたはノードがリーフの場合、-

  • 戻る

• ノードの値をretに挿入します

• ノードの左側が存在する場合、-

  • leftBoundary（ノードの左側）

• それ以外の場合

  • leftBoundary（ノードの右側）

• 関数rightBoundary（）を定義します。これはノードを取ります

• ノードがnullまたはノードがリーフの場合、-

  • 戻る

• ノードの値をretに挿入します

• ノードの右側が存在する場合、-

  • rightBoundary（ノードの左側）

• それ以外の場合

  • rightBoundary（ノードの右側）

• 関数leaves（）を定義します。これはノードを取ります

• ノードが存在しない場合、-

  • 戻る

• ノードがリーフの場合、-

  • ノードのvalをretに挿入します

• 葉（ノードの左側）

• 葉（ノードの右側）

• メインの方法から、次のようにします-

• ret配列をクリアします

• ルートが存在しない場合、-

  • retを返す

• ルートのvalをretに挿入します

• leftBoundary（ルートの左側）

• 葉（ルートの左側）;

• 葉（ルートの右）;

• rightBoundary（ルートの権利）

• retを返す

例

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<auto> v){
   cout << "[";
   for(int i = 0; i<v.size(); i++){
      cout << v[i] << ", ";
   }
   cout << "]"<<endl;
}
class TreeNode{
   public:
      int val;
      TreeNode *left, *right;
      TreeNode(int data){
         val = data;
         left = NULL;
         right = NULL;
      }
};
void insert(TreeNode **root, int val){
   queue<TreeNode*> q;
   q.push(*root);
   while(q.size()){
      TreeNode *temp = q.front();
      q.pop();
      if(!temp->left){
         if(val != NULL)
            temp->left = new TreeNode(val);
         else
            temp->left = new TreeNode(0);
         return;
      }else{
         q.push(temp->left);
      }
      if(!temp->right){
         if(val != NULL)
            temp->right = new TreeNode(val);
         else
            temp->right = new TreeNode(0);
         return;
      }else{
         q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
class Solution {
public:
   vector<int> ret;
   void leftBoundary(TreeNode* node){
      if (!node || node->val == 0 || (!node->left && !node->right))
         return;
      ret.push_back(node->val);
      if (node->left && node->left->val != 0)
         leftBoundary(node->left);
      else
         leftBoundary(node->right);
   }
   void rightBoundary(TreeNode* node){
      if (!node || node->val == 0 || (!node->left && !node->right))
         return;
      if (node->right && node->right->val != 0) {
         rightBoundary(node->right);
      }
      else {
         rightBoundary(node->left);
      }
      ret.push_back(node->val);
   }
   void leaves(TreeNode* node){
      if (!node || node->val == 0)
         return;
      if (!node->left && !node->right) {
         ret.push_back(node->val);
      }
      leaves(node->left);
      leaves(node->right);
   }
   vector<int> boundaryOfBinaryTree(TreeNode* root){
      ret.clear();
      if (!root)
         return ret;
      ret.push_back(root->val);
      leftBoundary(root->left);
      leaves(root->left);
      leaves(root->right);
      rightBoundary(root->right);
      return ret;
   }
};
main(){
   Solution ob;
   vector<int> v = {1,2,3,4,5,6,NULL,NULL,NULL,7,8,9,10};
   TreeNode *root = make_tree(v);
   print_vector(ob.boundaryOfBinaryTree(root));
}

入力

{1,2,3,4,5,6,NULL,NULL,NULL,7,8,9,10}

出力

[1, 2, 4, 7, 8, 9, 10, 6, 3, ]