C++の無向グラフの連結成分すべての最小要素の合計

この問題では、arr [i]が（i + 1）番目のノードを表すN個の数値の配列arrが与えられます。また、エッジのMペアがあり、uとvはエッジによって接続されたノードを表します。私たちのタスクは、無向グラフのすべての連結成分の最小要素の合計を見つけるプログラムを作成することです。ノードが他のノードに接続されていない場合は、1つのノードを持つコンポーネントとしてカウントします。

問題を理解するために例を見てみましょう

入力

arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5

出力

8

説明

以下は上に描かれたグラフです-

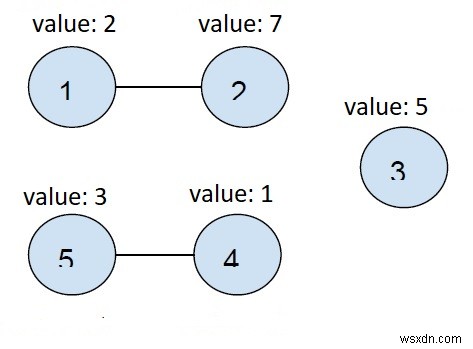
2つの接続されたノードと1つの単一ノードがあります

それでは、接続されているすべてのコンポーネントを最小限に抑えましょう

最小（ノード1およびノー​​ド2）=最小（2、7）=2

最小（ノード4およびノー​​ド5）=最小（1、3）=1

最小（ノード3）=最小（5）=5

合計=1+ 2 + 5 =8

この問題を解決するために、トラバーサル手法（BFSまたはDFS）のいずれかを使用して、無向グラフの接続されたすべてのノードを見つけ、二重訪問がないために訪問されたすべてのノードの訪問済み配列を作成します。直接または間接的に接続されている接続されたノードにアクセスすると、すべての接続の最小値が見つかります。そして、sum変数のこの最小値を追加します。すべてのノードにアクセスしたら、合計を出力します。

例

ソリューションの動作を説明するプログラム

#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
   minimum = min(minimum, arr[node]);
   visited[node] = true;
   for (int i : graph[node]) {
      if (!visited[i])
         dfs(i, arr, minimum);
   }
}
void createEdge(int u, int v){
   graph[u - 1].push_back(v - 1);
   graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
   int sum = 0;
   for (int i = 0; i < n; i++) {
      if (!visited[i]) {
         int minimum = arr[i];
         dfs(i, arr, minimum);
         sum += minimum;
      }
   }
   return sum;
}
int main(){
   int arr[] = {2, 7, 5, 1, 3};
   createEdge(1, 2);
   createEdge(4, 5);
   int n = sizeof(arr) / sizeof(arr[0]);
   cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
   cout<<minSum(arr, n);
   return 0;
}

出力

The sum of minimum elements in all connected components of an undirected graph is 8