データ構造のヒープへの挿入と削除
ここでは、バイナリヒープデータ構造から要素を挿入および削除する方法を説明します。最初のツリーが次のようになっていると仮定します-
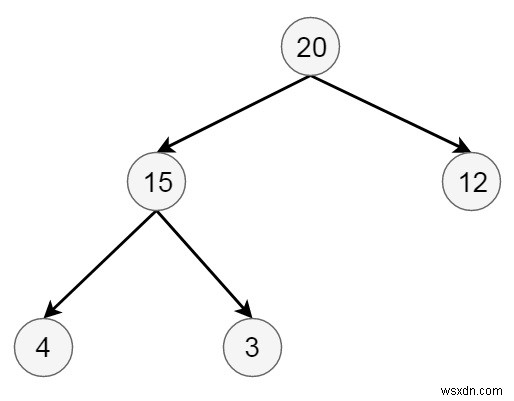
挿入アルゴリズム
insert(heap, n, item): Begin if heap is full, then exit else n := n + 1 for i := n, i > 1, set i := i / 2 in each iteration, do if item <= heap[i/2], then break heap[i] = heap[i/2] done end if heap[i] := item End
例
30をヒープに挿入するとします-
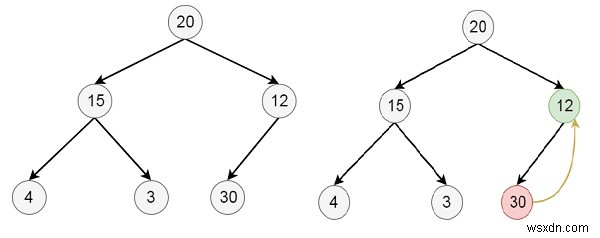
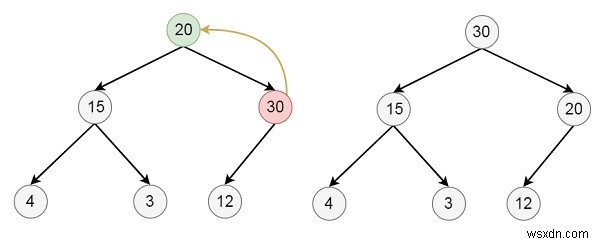
削除アルゴリズム
delete(heap, n): Begin if heap is empty, then exit else item := heap[1] last := heap[n] n := n – 1 for i := 1, j := 2, j <= n, set i := j and j := j * 2, do if j < n, then if heap[j] < heap[j + 1], then j := j + 1 end if if last >= heap[j], then break heap[i] := heap[j] done end if heap[i] := last End
例
最後のヒープから30を削除したいとします-
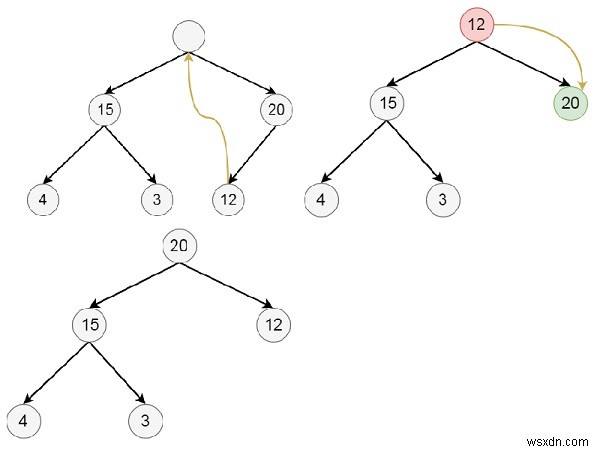
-
データ構造のインターバルヒープ
ここでは、間隔ヒープとは何かを確認します。間隔ヒープは完全な二分木であり、最後のノードを除く各ノードには2つの要素が含まれている可能性があります。ノードPの2つの要素の優先順位を「a」と「b」とします。ここでは、≤bを検討しています。ノードPは閉区間[a、b]を表すと言います。ここで、aはPの区間の左端であり、bは右端です。 [c、d]は、a≤c≤d≤bの場合に限り、区間[a、b]に含まれます。区間ヒープでは、各ノードPの左右の子で表される区間は、Pで表される区間に含まれます。最後のノードに優先度cの単一要素が含まれている場合、a≤c≤bです。ここで、[a、b]は最後のノードの親の間隔です。
-
データと構造の独立性
構造的独立性 データベース構造の変更がデータにアクセスするDBMSの機能に影響を与えない場合、構造的な独立性が存在します。 データベース構造の変更がデータにアクセスするDBMSの機能に影響を与えない場合、構造的な依存関係が存在します。 データの独立性 下位レベルで行われた変更は、上位レイヤーには影響しません。 2つのタイプは-です 物理データの独立性 論理データの独立性 物理データの独立性から始めましょう- 物理データの独立性 スキーマまたは論理データに影響を与えずに物理スキーマを変更します。達成するのは簡単です。 これは、データベースの内部レベルと、論理レベルから内
