データ構造における加重グラフ表現
グラフはさまざまなバリエーションに分類できることがわかっているので、それらは、有向または無向にすることができ、加重または非加重することができます。ここでは、メモリ内の重み付きグラフを表す方法を説明します。次のグラフを検討してください-
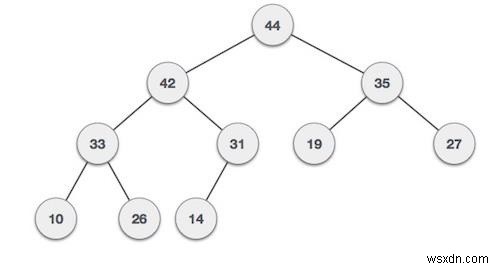
隣接行列表現
隣接行列形式を使用して加重グラフを格納するために、行列をコスト行列と呼びます。ここで、位置M [i、j]の各セルは、エッジiからjまで重みを保持しています。エッジが存在しない場合、それは無限大になります。同じノードの場合、0になります。
| 0 | ∞ | 6 | 3 | ∞ |
| 3 | 0 | ∞ | ∞ | ∞ |
| ∞ | ∞ | 0 | 2 | ∞ |
| ∞ | 1 | 1 | 0 | ∞ |
| ∞ | 4 | ∞ | 2 | 0 |
隣接リストでは、リスト内の各要素に2つの値があります。最初のノードは宛先ノードであり、2番目のノードはこれら2つのノード間の重みです。表現は以下のようになります。
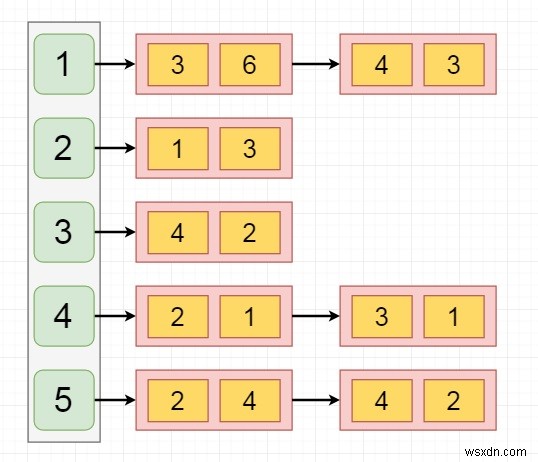
-
ハーフエッジデータ構造
はじめに テンプレートパラメータまたはハーフエッジデータ構造(HalfedgeDSと略記)のHDSは、平面マップ、多面体、またはその他の方向付け可能な2次元など、頂点、エッジ、および面の入射情報を維持できるエッジ中心のデータ構造として定義されます。ランダムな次元に埋め込まれたサーフェス。各エッジは、反対方向の2つのハーフエッジに分割されます。各ハーフエッジには、1つの入射面と1つの入射頂点が格納されます。各面と各頂点に1つの入射ハーフエッジが格納されます。ハーフエッジデータ構造のバリエーションを減らすと、面のハーフエッジポインタや面の保存など、この情報の一部を削除できます。 ハーフエッジデ
-
データ構造の隣接リスト
グラフは非線形のデータ構造です。これは、ノードを使用したデータと、エッジを使用したそれらの関係を表します。グラフGには2つのセクションがあります。頂点とエッジ。頂点はセットVを使用して表され、エッジはセットEとして表されます。したがって、グラフ表記はG(V、E)です。アイデアを得るための1つの例を見てみましょう。 このグラフには、5つの頂点と5つのエッジがあります。エッジが方向付けられます。例として、頂点BとDを接続するエッジを選択した場合、ソース頂点はBで、デスティネーションはDです。したがって、BをDに移動することはできますが、DからBに移動することはできません。 グラフは非線形
