最短経路のためのベルマンフォードアルゴリズム

ベルマンフォードアルゴリズムは、ソース頂点から他の頂点までの最小距離を見つけるために使用されます。このアルゴリズムとダイクストラのアルゴリズムの主な違いは、ダイクストラのアルゴリズムでは負の重みを処理できないことですが、ここでは簡単に処理できます。

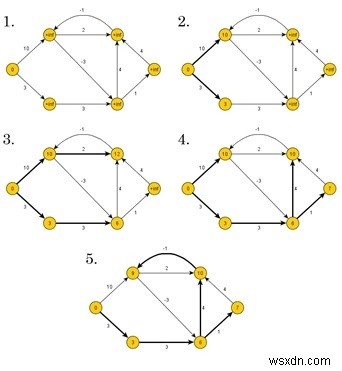
Bellman-Fordアルゴリズムは、ボトムアップ方式で距離を検出します。最初に、パスにエッジが1つしかない距離を見つけます。その後、パスの長さを増やして、考えられるすべての解決策を見つけます。

入力と出力

Input:
The cost matrix of the graph:
0  6  ∞ 7  ∞
∞  0  5 8 -4
∞ -2  0 ∞  ∞
∞  ∞ -3 0  9
2  ∞  7 ∞  0

Output:
Source Vertex: 2
Vert:   0   1   2   3   4
Dist:  -4  -2   0   3  -6
Pred:   4   2  -1   0   1
The graph has no negative edge cycle

アルゴリズム

bellmanFord(dist, pred, source)

入力- 距離リスト、先行リスト、およびソース頂点。
出力- 確かに、負のサイクルが見つかった場合。

Begin
   iCount := 1
   maxEdge := n * (n - 1) / 2     //n is number of vertices

   for all vertices v of the graph, do
      dist[v] := ∞
      pred[v] := ϕ
   done

   dist[source] := 0
   eCount := number of edges present in the graph
   create edge list named edgeList

   while iCount < n, do
      for i := 0 to eCount, do
         if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) pred[edgeList[i].v] := edgeList[i].u
      done
   done

   iCount := iCount + 1
   for all vertices i in the graph, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i),
         then return true
   done

   return false
End

例

#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//Cost matrix of the graph (directed) vertex 5

int costMat[V][V] = {
   {0, 6, INF, 7, INF},
   {INF, 0, 5, 8, -4},
   {INF, -2, 0, INF, INF},
   {INF, INF, -3, 0, 9},
   {2, INF, 7, INF, 0}
};

typedef struct {
   int u, v, cost;
}edge;

int isDiagraph() {

   //check the graph is directed graph or not

   int i, j;
   for(i = 0; i<V; i++) {
      for(j = 0; j<V; j++) {
         if(costMat[i][j] != costMat[j][i]) {
            return 1;      //graph is directed
         }
      }
   }
   return 0;//graph is undirected
}

int makeEdgeList(edge *eList) {
   //create edgelist from the edges of graph
   int count = -1;
   if(isDiagraph()) {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<V; j++) {
            if(costMat[i][j] != 0 && costMat[i][j] != INF) {
               count++;         //edge find when graph is directed
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }else {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<i; j++) {
            if(costMat[i][j] != INF) {
               count++;         //edge find when graph is undirected
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }
   return count+1;
}

int bellmanFord(int *dist, int *pred,int src) {
   int icount = 1, ecount, max = V*(V-1)/2;
   edge edgeList[max];

   for(int i = 0; i<V; i++) {
      dist[i] = INF;      //initialize with infinity
      pred[i] = -1;      //no predecessor found.
   }

   dist[src] = 0;//for starting vertex, distance is 0

   ecount = makeEdgeList(edgeList);       //edgeList formation

   while(icount < V) {       //number of iteration is (Vertex - 1)
      for(int i = 0; i<ecount; i++) {
         if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {      //relax edge and set predecessor
            dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
            pred[edgeList[i].v] = edgeList[i].u;
         }
      }
      icount++;
   }

   //test for negative cycle
   for(int i = 0; i<ecount; i++) {
      if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {
         return 1;    //indicates the graph has negative cycle
      }
   }

   return 0;     //no negative cycle
}

void display(int *dist, int *pred) {
   cout << "Vert: ";
   for(int i = 0; i<V; i++)
      cout <<setw(3) << i << " ";
   cout << endl;
   cout << "Dist: ";

   for(int i = 0; i<V; i++)
      cout << setw(3) << dist[i] << " ";
   cout << endl;
   cout << "Pred: ";

   for(int i = 0; i<V; i++)
      cout << setw(3) << pred[i] << " ";
   cout << endl;
}

int main() {
   int dist[V], pred[V], source, report;
   source = 2;
   report = bellmanFord(dist, pred, source);
   cout << "Source Vertex: " << source<<endl;
   display(dist, pred);

   if(report)
      cout << "The graph has a negative edge cycle" << endl;
   else
      cout << "The graph has no negative edge cycle" << endl;
}

出力

Source Vertex: 2
Vert:   0   1   2   3   4
Dist:  -4  -2   0   3  -6
Pred:   4   2  -1   0   1
The graph has no negative edge cycle