負の整数を持つマイクロプロセッサのロマンス – CPU 算術設計の方法と理由
コンピュータについて最初に学ぶことの 1 つは、0 と 1 しか理解できないということです。 、 またはビット .
一方、私たち人間は 10 進法を使って数字をやり取りします。このシステムでは、0 から 9 までの数字とプラス記号とマイナス記号 (+ と -) を使用して、正または負の数を示します。
コンピュータは 2 桁しか使用できないため – 0 と 1 – 昔のエンジニアと数学者は、負の数を表し、それを使って算術を行う巧妙なテクニックを考案しました。これらのテクニックの美しさを探ってみましょう。
まず、コンピューターの仕組みに関する背景
ソフトウェア、画像、テキスト、ビデオ、数字、およびその間のすべては、コンピューターの最低レベルで 0 と 1 です。
画像、テキスト、ビデオ、および数値については、これらのものを 0 と 1 にする方法を決定するエンコード スキームがあります。たとえば、テキストの ASCII と Unicode。
私たちがコーディングするソフトウェア プログラムは、コンパイラとアセンブラを介して 0 と 1 を取得します。機械語 (または機械命令) と呼ばれる 0 と 1 のセットは、プロセッサが実行する前に、まずコンピュータのメイン メモリ (RAM) に格納されます。
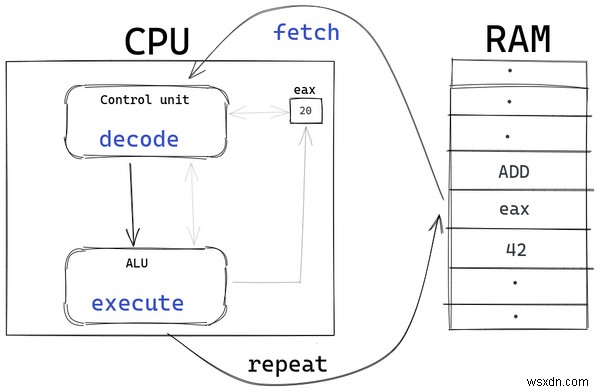
プロセッサはフェッチによって実行サイクルを開始します メインメモリからの命令、次にプロセッサの制御ユニットがデコードします これらの命令は、操作コード (opcode) とオペランドの 2 つの部分に分けられます。
オペコードは、ADD (加算)、JMP (ジャンプ)、INC (インクリメント) など、実行する必要がある追加のアクションを決定します。オペランドは、その操作が実行される値 (またはメモリ位置) です。
デコードされた命令は、実行のために算術論理演算ユニット (ALU) に送信されます。 . ALU では、オペランドのオペコードに基づいて命令が実行され、結果がメモリに格納されます。
たとえば、アセンブリ コード ADD eax, 42 アセンブラによって最初に機械語 (0 と 1) に変換されます。次に、フェッチ - デコード - 実行サイクルが開始される前に、メイン メモリに格納されます。
ADD eax, 42 のマシンコードの取得時 メモリが終了すると、命令がデコードされます。デコードされた出力は、オペコードが ADD であることを示しています オペランドは eax です と 42 .
eax レジスタは、プロセッサが瞬時にアクセスできるプロセッサに組み込まれたメモリ位置です。 eax レジスタは、ほとんどのプロセッサでアキュムレータと呼ばれます。
ADD eax, 42 アセンブリ コードは、eax の現在の値に 42 を追加するように設計されています。 登録 (アキュムレータ) し、その合計を eax に格納します . eax = eax + 42です .
現在 eax であるとします。 20 です。これは、eax の値が ADD eax, 42 を実行した後 20 + 42 =62 になります。

EDVAC などの初期のコンピューターの設計は、面倒な数学的計算をより簡単かつ迅速に行いたいという欲求から始まりました。
コンピューターに計算させる全責任は、加算器 (2 つの数値を加算する回路) の肩にかかっています。これは、減算、乗算、除算などの高度な演算が回路内で加算器を使用するためです。
究極的には、コンピューターは論理機能を備えた高速な計算機にすぎません。バイナリ算術設計 (正の整数、特に負の整数) の課題と美しさを理解することは、コンピュータ プロセッサの最も基本的な概念の 1 つです。 .
最初に、10 進数が 2 進数でどのように表されるか、および 2 つの 2 進数値を加算する方法を見てみましょう。それから私たちは美しさを探求し始めます。
バイナリ システムのしくみ
872500 と読むように言ったら 、おそらく 872.5K と言うでしょう .私たちの心がどのようにこれを行うかを見てみましょう.
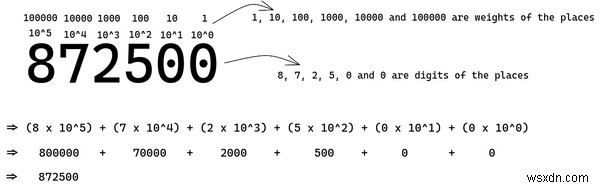
1 の位を右から 1 桁目に、10 の位を右から 2 番目に、100 分の 1 を 3 番目に、というように 10 の累乗ずつ増やします。
これらの各場所の 10 のべき乗は、場所の重みです。 100 位の重みは 100 です。各桁の数字にその桁の重みを掛けて合計し、完全な数を取得します。
上の図では、各場所の重みの増加が、10^0 から始まる 10 の累乗であることがわかります。 そして 10^5 を通過します .そのため、小数は基数 10 システムと呼ばれます。

バイナリでは、各場所の重みは 2 の累乗で増加します。これは、場所の重みが 2^0 から始まることを意味します。 2^something で終わります .それが唯一の違いです。
00110101 10 進数では 53 に変換されます。コンピューターは、人間が 10 進数を解釈するのと同じ方法で 2 進数を解釈します。つまり、各桁の数字に重みを掛けて合計します。
1 と 0 を追加する方法
足し算は、10 進数で行われるのとほとんど同じように 2 進数で機能します。例を通してそれを見てみましょう。 2 つの 2 進数を追加します:1101 (13) と 1100 (12).
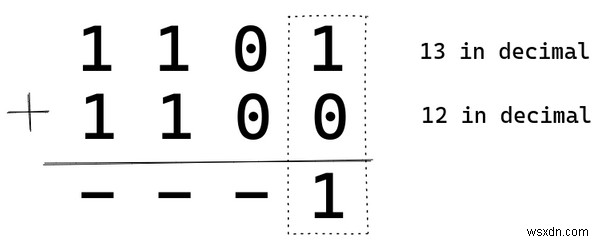
10 進法と同じように、1 の位 (2^0) から始めます。 )。 1 と 0 を足すと 1 になるので、そこに 1 を置きます。私と一緒にいれば、全体像がわかります。
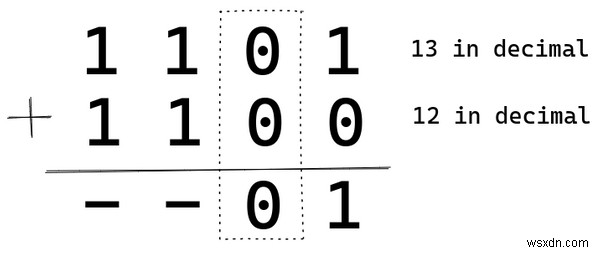
0 プラス 0 は 0 です。次に進みます。
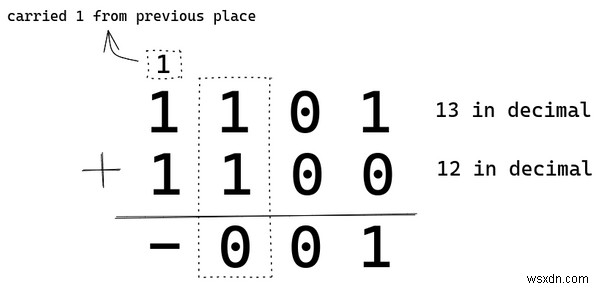
1 たす 1 は 2 です。2 進数の 2 は 10 として表されます。 . 1 を次の桁に繰り上げ、現在の桁の結果として 0 を保持しています。
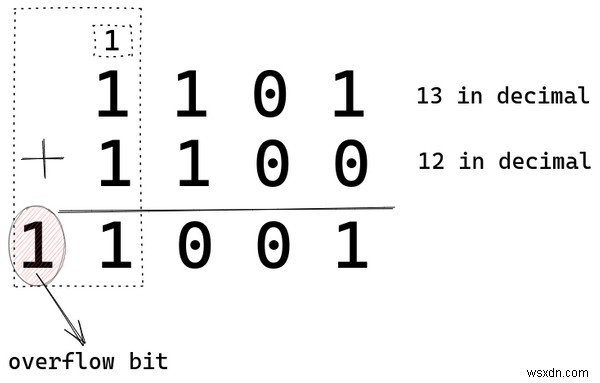
そこには 1 が 2 つと、前の場所から繰り越された 1 が 1 つあるので、合計 3 つの 1 があります。それらの合計は 3 になり、バイナリの 3 は 11 です。 だから 11 と書く .最終結果は 11001 になります または 10 進形式で 25、実際には 13 + 12 です。
上記の計算では、結果を格納するために 5 ビットを使用できると仮定しています。 4 ビットのコンピューターがこの加算を行う場合、結果を格納するために使用できるのは 4 ビットのみです。
その 5 番目のビットは オーバーフロー と呼ばれます 4ビットコンピュータで。整数演算では、オーバーフロー ビットは無視または破棄されます。したがって、1001 となります。 (9) 4 ビット コンピューターを使用した場合の結果として。
バイナリ演算設計の美しさ
先に進む前に理解しておく必要がある 2 つの重要な用語は、最下位ビットです。 と最上位ビット .

一番右のビットが最下位ビットです 場所の重みが最小であるため (2^0) )。そして、一番左のビットが最上位ビットです 場所の重みが最も高いため (2^7 ).
世界に正の数しかない場合、これでこの記事は終わりです (小数を 2 進数で表す方法と、それらを 2 進数で加算する方法を既に学習したため)。
ありがたいことに、負の数もあります。
CPU の演算設計の美しさは、ネガティブなところにあります。
では、コンピューターはどのように負の数を表し、負の数の演算はどのように機能するのでしょうか?この問題に対するエンコーディングのアプローチを見てみましょう。
以下のセクションでは、概念を理解するために 4 ビット コンピュータを使用します。つまり、5 番目のビットはオーバーフローとして扱われます。演算を行うための 16 ビット、32 ビット、64 ビットなど、すべての CPU アーキテクチャに同じ原則が適用されます。
符号マグニチュード エンコーディング アプローチ
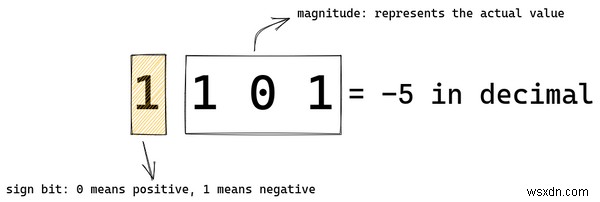
1101 10 進形式では、このコード化スキームでは -5 になります。左端または最上位ビットは符号ビットです。数値の符号、つまり数値が正か負かをプロセッサに伝えます。
0 符号ビットの は正の値を表し、1 負の値を表します。残りのビットは、実際の大きさを示しています。
1101 で 、符号ビットは 1 です 、したがって、数値は負です。 101 10 進数では 5 です。だから 1101 10 進数で -5 に計算されます。

上の図では、このエンコーディング アプローチを使用して 4 ビットで表現できるすべての整数を確認できます。この時点まではすべて良さそうです。
しかし、よく見ると、このエンコード スキームには非常に深刻な設計上の問題があることがわかります。その問題に直面しましょう。
正の数と負の数を足してみましょう。たとえば、+4 と -1 を追加します。答えは (+4) + (-1) = (+3) になるはずです 0011 です .
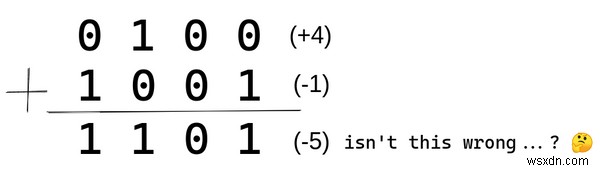
ほら、結果は 1101 です (-5)。実際の答えは 0011 のはずです (+3)。このアプローチをプロセッサに実装する場合、この問題に対処するためにロジックを追加する必要があり、エンジニアはロジックが複雑になることを嫌います。
回路を追加すると、消費電力が増加し、パフォーマンスが低下します。
これは、最新のトランジスタ ベースのコンピューターにとっては些細な問題のように聞こえるかもしれません。
しかし、EDVAC のような初期のコンピューターを考えてみてください。EDVAC は、1 日に何百人もの人々によって操作され、キロワット単位で電力を消費する何千もの真空管で動作していました。そして政府はそれらを建設するために何百万ドルも費やしました。
当時、追加の回路と真空管を追加するには数千ドルが必要であり、メンテナンスに深刻な問題がありました。
そのため、エンジニアはよりスマートなエンコーディング設計を考えなければなりませんでした。
今こそ、この問題に取り組み、システムをよりシンプルにし、パフォーマンスを向上させ、消費電力を削減する美しさを明らかにする時が来ました.
美しいエンコーディング システムが入り、CPU が輝きます❤️
このエンコーディング スキームでは、前のコードと同様に、左端のビットが符号ビットとして機能しますが、負の数を表すためにいくつかの技術が必要です。
正の数は、前のエンコード方式とまったく同じ方法で表されます:先頭の 0 大きさの残りのビットが続きます。たとえば、このコード化スキームでも、6 は 0110 として表されます。 .
負の数を表すために、2 段階の数学プロセスが正の数で実行されます。 -6 を表すということは、+6 に対して 2 段階の数学プロセスを実行して、バイナリで -6 を取得するということです。
-6 がバイナリにエンコードされる方法を見てみましょう:

前の符号の大きさのアプローチでは、負の +6 を計算するには、符号ビットを 0 から変更するだけでした。 1 へ . 0110 (+6) は 1110 になります (-6).
この新しいエンコード方式では、まずビットを反転します。 0 を 1 に、1 を 0 に変更します。 0110 (+6) は 1001 になります .ビットを反転することを「1 の補数」と呼ぶので、ここでは 0110 の 1 の補数を計算しました。 結果は 1001 になります .それから...

0001 を追加します (+1) をステップ 1 で取得した 1 の補数 (1001) に )。結果 1010 -6 のバイナリ表現になります。このエンコード方式は、2 の補数と呼ばれます。 したがって、正の整数の 2 の補数を計算すると、対応する負の整数が得られることに注意してください。
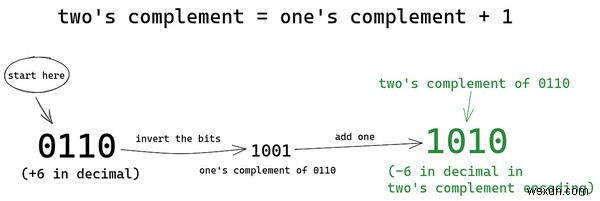
ビットを反転すると、1 の補数が得られます。 1 の補数に 1 を追加すると、元のビットの 2 の補数が得られます。簡単ですよね?

では、このエンコーディング スキームが非常に美しい理由を見てみましょう。 0100 を追加します (+4) と 1111 (-1).
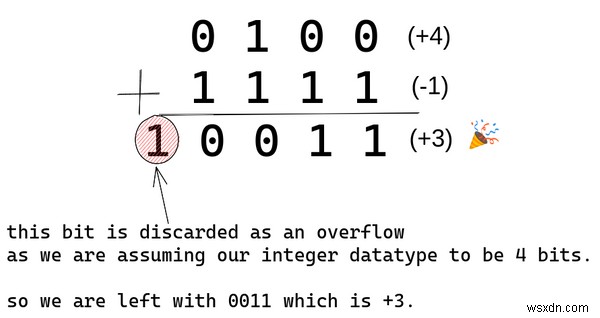
ほら、2 の補数エンコード方式で正確な結果が得られます。これで、符号を気にせずに整数を追加できます。
2 の補数エンコーディングを使用して、負の整数を 0 と 1 で表現する方法を学習しました。 ADD eax, -3 を実行するとします。 eax レジスタの現在の値は -1 です。したがって、ADD eax, -3 の実行後の eax の値は -4 になります (これは 1100 です) 2 の補数エンコーディングで)。
オペレーティング システムが 1100 を取得したとき eax からユーザーに結果を提示するために、オペレーティング システムはどのように 1100 をデコードしますか? 十進数に?または、プログラマーとして 1100 に遭遇したとします。 、1100 の数をどうやって割り出すことができますか? 表す?
もちろん、1100 にいつ到達するかを確認するために、各正の整数の 2 の補数を計算し続けることはできません。 .それは遅すぎるでしょう。
プログラマーと OS は、2 の補数の美しい特性を使用して、2 進数を 10 進数にデコードします。
正の数の 2 の補数を計算すると、対応する負の数が得られます。 逆もまた然り – つまり、負の数の 2 の補数を計算すると、対応する正の数が得られます。この理由はすぐにわかります。
まず、OS またはプログラマーが 1100 をデコードする方法を理解しましょう。

1100 の取得時 eax レジスタから、OS は 1 を認識します。 整数が負であることを知らせる符号ビットとして。 1100 の 2 の補数 1100 の正の対応物を与えるように計算されます 0100 として出力されます (+4)。次に、OS は対応する正の符号に負の符号を付加し、最終的な答えを -4 として返します。この段落をもう一度読み直すと、理解が深まります。
その後、CPU は笑顔で今日の美しさに別れを告げます;)
CPUは母親に会うために家に行きました。 2 の補数の芸術の内部の仕組みについて議論する十分な時間があります。
2 の補数エンコードが機能する理由と仕組み
+42 などの負の数を求める場合、+42 の負の数を求める最も簡単な方法は何ですか?
おそらく、最も簡単な方法は、0 から数値を引くことですよね? 0 - (+42) = -42 .これを繰り返すと、正の値 0 - (-42) = +42 に戻ります。 .これは、2 の補数が構築されるすべての数学です。

10000 を実行しています (左端の 1 がオーバーフローであるため、10 進数で 0) マイナス 0101 (+5)。 1011 を取得します つまり、2 の補数エンコードでは 10 進数で -5 です。減算がどのように行われるかは無視してください。それは重要ではありません。 2 の補数の背後にある直感を理解することが重要です。
10000 1111 + 0001 のように記述できます (これら 2 つを追加してみると、10000 が得られます )。実際に行っていること:
10000 - 0101
=> (1111 + 0001) - 0101
上記の方程式を整理すると、次のように書くことができます:
(1111 + 0001) - 0101
=> (1111 - 0101) + 0001
Step 1: subtract 0101 from 1111
1 1 1 1
-0 1 0 1
---------
1 0 1 0
see, subtracting 0101 from 1111 is equivalent
to inverting the bits of 0101, as we got 1010 as a result.
Step 2: add 0001 to the above result
1 0 1 0 ---> result of step 1
+0 0 0 1
---------
1 0 1 1
we get 1011 that is -5 in two's complement encoding.
2 の補数システムは基本的に 0 から数を引いたものであることがわかりましたか?ビットを反転して 1 を加算することは、0 から数を減算するための高速で賢い方法です。
これが、2 の補数を計算するときに、負の数の正数と正の数の負数を取得する理由です。これは、実際には 0 から数を減算しているためです (0 - number )。
1900 年代のコンピューターは、2 の補数符号化スキームが非常に美しく、減算が簡単に実行できるため、加算算術ロジックのみを使用していました。
たとえば、100 から 12 を引くには、CPU が +12 の 2 の補数を計算して -12 を生成し、次に 100 に -12 を足して、必要な出力を得ます。
0 から直接減算して、2 進数で負の数を見つけたり、その逆を行ったりしないのはなぜですか?
引き算は時間がかかり複雑なプロセスなので (借用のおかげです)、その方法を使用する場合、コンピュータには高価な引き算回路が必要になります。負の整数を表現するたびに 0 から減算することを想像してみてください。私たちにとっても、コンピューターにとっても悪夢になるでしょう!
2 の補数エンコーディングは、よりパフォーマンスの高いソリューションであり、回路設計が単純になり、多くの費用を節約できます。これは、減算に高価な回路が必要なく、+ と - の整数の演算を処理する追加のロジックがないためです。単純な足し算で、足し算と引き算の両方を行うことができます。
では、この美しいエンコード スキーム (2 の補数 ❤️) について、コンピューター デザイナーに感謝しましょう。
最後の言葉
私は、自分が作成した教材に対して決して料金を請求しないと自分に約束しました。単純な記事であれ、コースであれ、電子ブックであれ、私が教育のために行うことは、常に 100% 自由でオープンです。
Twitter アカウントで役立つリソースを投稿し、有意義な考えを共有しています。この記事から何か新しいことを学んだ場合は、私をフォローして DM を送ってください。それは私の一日を作るでしょう:)
すべての開発者、すべての作成者、すべての人間が誰かから学びます。私たちが学ぶ人々やリソースは引用され、広められるべきだと私は信じています。これにより、それらの善良な人々が私たち全員のためにもっと多くのことをするようになります.これが私の良いものです。
mycodeschool の Animesh は、この記事で書いた概念を含め、他の誰よりも多くのプログラミング概念を教えてくれました。
私のメンターであり友人である André Jaenisch のレビューと絶え間ないサポートがなければ、この記事を書くことはなかったでしょう。
楽しく学習しましょう!
-
Redis SADD –セットに要素を作成して追加する方法
このチュートリアルでは、コマンド– SADD を使用して、キーに格納されている設定値に要素を作成および追加する方法について学習します。 redis-cliで。キーがデータストアに存在する場合、指定されたすべての要素がセットに追加されます(すでに存在する要素は無視されます)。そうでない場合は、セットに追加する前に新しいセットが作成されます。 redis SADDコマンドの構文は次のとおりです:- 構文:- redis host:post> SADD <key name> <value 1> [ <value 2> ] 出力:- - (integ
-
Windows 10 の自動再生オプションにアクセスして操作する方法
Windows にある最も古い機能の 1 つ オペレーティング システムは AutoPlay と呼ばれます . Windows 98、Windows XP から存在しています 次に Vista まで 、Windows 7 Windows 8、Windows 8.1 に引き継がれました そして今、Windows 10 に ! ただし、Windows のごく一部にすぎません ユーザーは、Windows を 1 つでも保存できるこの重要な機能に注目しています。 USB フラッシュ ドライブなどのポータブル ストレージ デバイスからのウイルスにマシンが感染するのを防ぎます。 およ
