C++でゼロに追加されるバランスBSTにトリプレットがあるかどうかを確認します

平衡二分探索木があるとすると、is_valid_triplet（）という名前の関数を作成する必要があります。この関数は、指定されたBSTに合計が0に等しいトリプレットが存在する場合はtrueを返し、そうでない場合はfalseを返します。 。これらの制約に従ってメソッドを設計します-

• 予想される時間計算量はO（n ^ 2）

• O（logn）余分なスペースを使用できます。

つまり、入力が次のような場合

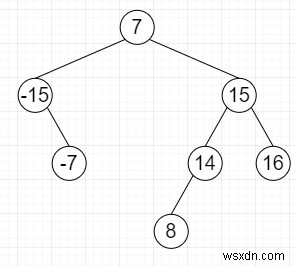
トリプレットは[-15,7,8]

これを解決するには、次の手順に従います-

• 関数bst_to_doubli_list（）を定義します。これにより、ルート、ヘッド、テールが取得されます

  。

• ルートがNULLと同じ場合、-

  • 戻る

• ルートの左側がnullでない場合、-

  • bst_to_doubli_list（ルート、ヘッド、テールの左側）

• ルートの左側：=テール

• tailがnullでない場合、-

  • 尾の右側：=ルート

• それ以外の場合

  • ヘッド：=ルート

• テール：=ルート

• ルートの権利がnullでない場合、-

  • bst_to_doubli_list（ルート、ヘッド、テールの右側）

• 関数is_in_double_list（）を定義します。これは、head、tail、sum、

  を取ります。

• 頭が尻尾と等しくない場合は、-

  • 現在：=頭のキー+尾のキー

  • 電流が合計と同じ場合、-

    • trueを返す

  • それ以外の場合、現在の>合計の場合、-

    • 尻尾：=尻尾の左側

  • それ以外の場合

    • 頭：=頭の右側

• falseを返す

• メインの方法から、次のようにします-

• ルートがnullの場合、-

  • falseを返す

• ヘッド=null

• tail =null

• bst_to_doubli_list（root、head、tail）

• （頭の右側が頭の尻尾とキー<0と等しくない）、実行-

  • is_in_double（頭の右、尾、頭のキー*（-1）の場合、

    • trueを返す

  • それ以外の場合

    • 頭：=頭の右側

• falseを返す

例（C ++）

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
class TreeNode {
   public:
   int key;
   TreeNode *left;
   TreeNode *right;
   TreeNode() : key(0), left(NULL), right(NULL) {}
   TreeNode(int x) : key(x), left(NULL), right(NULL) {}
};
void bst_to_doubli_list(TreeNode* root, TreeNode** head, TreeNode** tail) {
   if (root == NULL)
      return;
   if (root->left)
      bst_to_doubli_list(root->left, head, tail);
   root->left = *tail;
   if (*tail)
      (*tail)->right = root;
   else
      *head = root;
      *tail = root;
   if (root->right)
      bst_to_doubli_list(root->right, head, tail);
}
bool is_in_double_list(TreeNode* head, TreeNode* tail, int sum) {
   while (head != tail) {
      int current = head->key + tail->key;
      if (current == sum)
         return true;
      else if (current > sum)
         tail = tail->left;
      else
         head = head->right;
   }
   return false;
}
bool is_valid_triplet(TreeNode *root) {
   if (root == NULL)
      return false;
   TreeNode* head = NULL;
   TreeNode* tail = NULL;
   bst_to_doubli_list(root, &head, &tail);
   while ((head->right != tail) && (head->key < 0)){
      if (is_in_double_list(head->right, tail, -1*head->key))
         return true;
      else
         head = head->right;
   }
   return false;
}
TreeNode* insert(TreeNode* root, int key) {
   if (root == NULL)
      return new TreeNode(key);
   if (root->key > key)
      root->left = insert(root->left, key);
   else
      root->right = insert(root->right, key);
   return root;
}
int main(){
   TreeNode* root = NULL;
   root = insert(root, 7);
   root = insert(root, -15);
   root = insert(root, 15);
   root = insert(root, -7);
   root = insert(root, 14);
   root = insert(root, 16);
   root = insert(root, 8);
   cout << is_valid_triplet(root);
}

入力

root = insert(root, 7);
root = insert(root, -15);
root = insert(root, 15);
root = insert(root, -7);
root = insert(root, 14);
root = insert(root, 16);
root = insert(root, 8);

出力

1