C++でL={a bm a（n + m）-n、m≥1}のチューリングマシンを構築します

チューリングマシン −チューリングマシンは、タイプ0の文法によって生成された言語の単語を受け入れるために使用されるデバイスです。チューリングマシン（TM）は、入力が与えられるセルに分割された無限の長さのテープで構成される数学モデルです。入力テープを読み取るヘッドで構成されています。状態レジスタには、チューリングマシンの状態が格納されます。入力シンボルを読み取った後、別のシンボルに置き換えられ、内部状態が変更され、1つのセルから右または左に移動します。 TMが最終状態に達すると、入力文字列が受け入れられます。それ以外の場合は拒否されます。

TMは、正式には7タプル（Q、X、Σ、δ、q0、B、F）として記述できます。ここで-

• Qは有限の状態のセットです
• Xはテープのアルファベットです
• Σは入力アルファベットです
• δは遷移関数です。 δ：Q×X→Q×X×{Left_shift、Right_shift}。
• q0は初期状態です
• Bは空白の記号です
• Fは最終状態のセットです

私たちの目標は、言語を受け入れるチューリングマシンTMを構築することです

L =anbma（n + m）ここで、n、m> =1

TMが受け入れることができる単語の例を見てみましょう

• abaa、n =1、m =1
• aabaaa、n =2、m =1
• abbaaa、n =1、m =2
• aaabaaaa、n =3、m =1

つまり、aのn回、bのm回、aのn+m回が続きます。 n、m> =1

少なくともありません。 aのは常に3で、bは1です。両方ともn =m=1の場合。

アプローチは以下に要約されています-

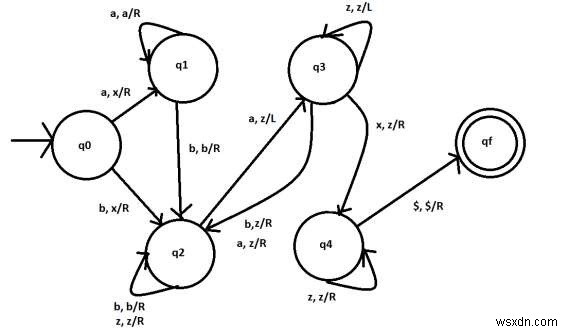
マシンは最初にすべてのn番号を受け入れます。 aの後にすべてのmnoが続きます。 bの。その後、さらに多くのaが検出されると、前の入力bとaの削除が開始されます。最終的に、新しいaが来ず、頭が最初の入力文字に到達すると、すべての文字が正しく処理されることを意味します。入力文字列のステップバイステップをたどってみましょう-

状態q0からの移行

• δ（q0、a）→（q1、x、R）。状態q0で、文字の読み取りが状態q1に移行する場合は、xにして右に移動し、文字列内の次の文字をポイントします。

  Ex − aabaaa→xabaaa（最初のキャラクターがx頭になり、次のaに右に移動）

• δ（q0、b）→（q3、x、R）。状態q0で、読み取られた文字が状態q3に移行する場合は、xにして右に移動し、文字列内の次の文字をポイントします。

  例−babaaa…。 →xabaaa…。 （最初のキャラクターがx頭になり、次のキャラクターに右に移動しました）

ここで、xは最初の文字を表すために使用されます。

状態q1からの移行

• δ（q1、a）→（q1、a、R）。状態q1で、読み取られた文字がtheの場合、状態q1のままになり、右に移動して文字列内の次の文字をポイントします。

  例：xaabaaa…→xaabaaa…（残りは何もせずに右に移動します）

• δ（q1、b）→（q2、b、R）。状態q1で、読み取られた文字がbの場合、状態q1のままで、右に移動して文字列内の次の文字をポイントします。

  例− xaabaaa…→xaabaaa…（残りのbは何もせずに右に移動します）

状態q2からの移行

• δ（q2、b）→（q2、b、R）。状態q2で、読み取られた文字がbの場合、状態q2のままで、右に移動して文字列内の次の文字をポイントします。

  例− xaabbbaaa…→xaabbbaaa…（残りのbは何もせずに右に移動します）

• δ（q2、z）→（q2、z、R）。状態q2で、読み取られた文字がzの場合、状態q2のままで、右に移動して文字列内の次の文字をポイントします。

  Ex − xaabaazz…→xaabaazz…（残りの場合、zは何もせずに右に移動します）

• δ（q2、a）→（q3、z、L）。状態q2で、文字の読み取りがaの場合、それをzにしてから、状態q3に移行し、左に移動して文字列内の前の文字をポイントします。

  Ex − xaabaazz…→xaabazzz…（aをzに置き換えて左に移動する場合）

状態q3からの移行

• δ（q3、z）→（q3、z、L）。状態q3で、読み取られた文字がzの場合、状態q3のままになり、左に移動して文字列内の前の文字をポイントします。

  Ex −xaabzzzz…→xaabzzzzz…（zの場合は何もせずに左に移動します）

• δ（q3、b）→（q2、z、R）。状態q2で、読み取られた文字がbの場合、それをzにして、stateq2でトランジットし、右に移動して文字列内の次の文字をポイントします。すべてのbを置き換えます

  Ex −xaabzzzz…→xaazzzzz…（bの場合はzに置き換えて右に移動します）

• δ（q3、a）→（q2、z、R）。状態q2で、文字の読み取りがaの場合、それをzにして、stateq3に遷移し、右に移動して文字列内の次の文字をポイントします。すべてを置き換えます

  Ex −xaazzzz…→xaazzzzz…（aをzに置き換えて右に移動する場合）

• δ（q3、x）→（q4、z、R）。状態q2で、読み取られた文字がxの場合はzにしてから、状態q3に移行し、右に移動して文字列内の次の文字をポイントします。最初のシンボルに到達しました。

  Ex −xzzzzzzz…→zzzzzzzz…（xの場合はzに置き換えて右に移動します）

状態q4からの移行

• δ（q4、z）→（q4 z、R）。状態q4で、読み取られた文字がzの場合、状態q4のままで、右に移動して文字列内の次の文字を指します。すべての文字がzになりました。

  例−zzzzzzzz…→zzzzzzzz…（すべてのzは何もせず、右に移動します）

• δ（q4、$）→（qf、$、R）。状態q4で文字が残っていない場合、終了に達しました。最終状態qfにトランジットします。これは、文字列が受け入れられることを意味します。

  Ex − zzzzzzzz $→zzzzzzzz（文字列の終わりの場合、$は何もせず、最終状態に移行します）

図はチューリングマシンを示しています-

入力

aabaaa
q0: aabaaa → q1: xabaaa → q1: xabaaa → q2: xabaaa → q3: xabzaa → q2: xazzaa
q2: xazzaa → q3: xazzza → q3: xazzza → q3: xazzza → q2: xzzzzza → q2: xzzzzza
q2: xzzzzza → q2: xzzzzza → q2: xzzzzza → q2: xzzzzzz → q3: xzzzzzz……..
q3: xzzzzzz → q3: xzzzzzz → q4: zzzzzzz → q4: zzzzzzz…….q4: xzzzzzz$ → qf: xzzzzzz$

qfに到達したということは、aabaaaが受け入れられたことを意味します