C++で重複する円と長方形

（radius、xc、yc）として表される円があると仮定します。ここで、（xc、yc）は円の中心座標です。また、（x1、y1、x2、y2）として表される軸に沿った長方形があります。ここで、（x1、y1）は左下隅の座標であり、（x2、y2）は右上隅の座標です。長方形の角。円と長方形が重なっていないか確認する必要があります。

したがって、入力が次のような場合

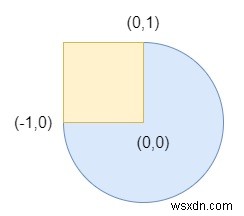
そうすれば、出力は真になります。

これを解決するには、次の手順に従います-

• 関数eval（）を定義します。これには、a、b、c、

  が必要です。

• bの最大値とaとcの最小値を返します

• メインの方法から、次のようにします-

• cdx：=eval（cx、left、right）、cdy：=eval（cy、bottom、top）

• rwid：=右-左、rh：=上-下

• dx：=cx-cdx、dy：=cy-cdy

• disSq：=（dx * dx）+（dy * dy）

• sqrRadius：=（r * r）

• disSq <=sqrRadiusの場合はtrueを返し、それ以外の場合はfalse

  を返します。

例

理解を深めるために、次の実装を見てみましょう-

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int eval(int a, int b, int c){
      return max(b, min(a, c));
   }
   bool checkOverlap(int r, int cx, int cy, int left, int bottom, int right, int top){
      double cdx = eval(cx, left, right);
      double cdy = eval(cy, bottom, top);
      double rwid = right - left;
      double rh = top - bottom;
      double dx = cx - cdx;
      double dy = cy - cdy;
      double disSq = (dx * dx) + (dy * dy);
      double sqrRadius = (r * r);
      return (disSq <= sqrRadius);
   }
};
main(){
   Solution ob;
   cout << (ob.checkOverlap(1, 0, 0, 1, -1, 3, 1));
}

入力

1, 0, 0, 1, -1, 3, 1

出力

1