データ構造における2つの最大HBLTの融合
メルド戦略は、再帰を使用して簡単に実行できます。 AとBが2つのHBLTであり、それらが融合するとします。それらの1つが空の場合は、最終結果として別の1つを作成するだけです。空のHBLTがない場合は、2つのルートの要素を比較する必要があります。より大きな要素を持つルートは、融合したHBLTのルートになります。
Aのルートが大きいとします。そして、それはその左側のサブツリーがLです。Cが最大HBLTであると仮定します。これは、AとHBLT Bの右側のサブツリーをマージした結果です。最終的なHBLTは、ルートとしてAを持ち、サブツリーとしてLとCを持ちます。 Lのs値がCの値よりも小さい場合、Cは基本的に左側のサブツリーです。それ以外の場合、Lはサブツリーのままになります。
-
のような2つの要素があるとします。 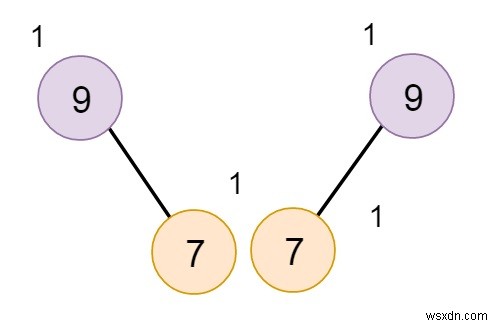
それらを融合させたい。 (ノードは値を保持しています。ノードの外側の数値は、対応するノードの値です。)
それでは、融合する方法を見てみましょう。 7が9の右の子として追加されたとしますが、ここでは、9のs(L)が0、9のs(R)が1であるため、それらは交換され、7がその右の子になります。

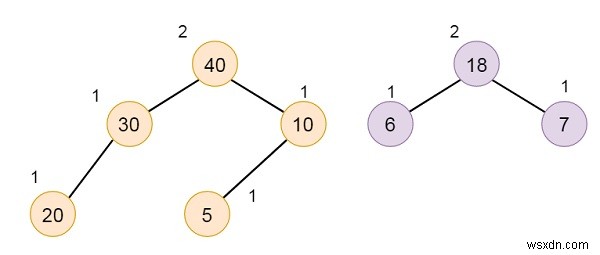
大きい方のHBLTの右側に、小さい方のHBLTを一時的に追加します。
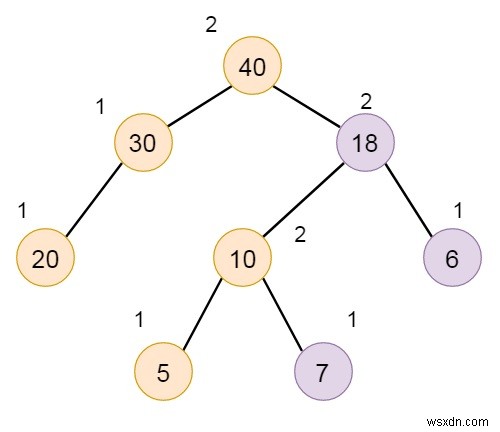
これはHBLTの特性を維持していません
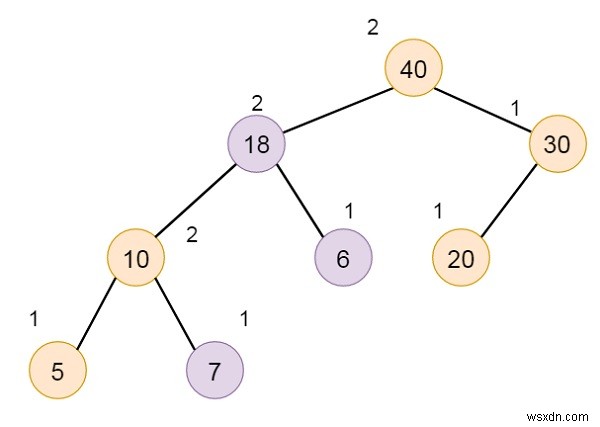
-
データ構造における高さバイアスの左翼ツリー
ここでは、Height Balanced Leftist Trees(HBLT)とは何かを確認します。 外部ノードと呼ばれる特別なノードがある二分木を考えてみましょう。 空の各サブツリーを置き換えます。他のすべてのノードは内部ノードと呼ばれます 。いくつかの外部ノードがいくつかのバイナリツリーとともに追加される場合、それは拡張バイナリツリーと呼ばれます。 。 このツリーの葉の端を考慮しない場合、それは実際の二分木です。これは拡張された二分木です。 ここで、 s(x) ノードxからそのサブツリー内の外部ノードまでの最短経路の長さです。 xが外部ノードの場合、その s(x) 値は0です。
-
ハーフエッジデータ構造
はじめに テンプレートパラメータまたはハーフエッジデータ構造(HalfedgeDSと略記)のHDSは、平面マップ、多面体、またはその他の方向付け可能な2次元など、頂点、エッジ、および面の入射情報を維持できるエッジ中心のデータ構造として定義されます。ランダムな次元に埋め込まれたサーフェス。各エッジは、反対方向の2つのハーフエッジに分割されます。各ハーフエッジには、1つの入射面と1つの入射頂点が格納されます。各面と各頂点に1つの入射ハーフエッジが格納されます。ハーフエッジデータ構造のバリエーションを減らすと、面のハーフエッジポインタや面の保存など、この情報の一部を削除できます。 ハーフエッジデ
