隣接リスト表現のためのダイクストラのアルゴリズム

隣接リスト表現を含む特定のグラフG（V、E）があり、ソース頂点も提供されます。ソース頂点からグラフGの他の頂点までの最短最短経路を見つけるダイクストラのアルゴリズム。

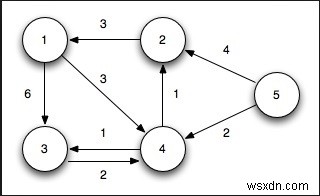
この問題を解決するために、2つのリストを使用します。 1つは最短経路ツリーと見なされている頂点を格納することであり、もう1つはまだ考慮されていない頂点を保持することです。アルゴリズムの各フェーズで、考慮されていない頂点が見つかり、ソースからの距離が最小になります。

別のリストは、先行ノードを保持するために使用されます。先行ノードを使用して、送信元と宛先からのパスを見つけることができます。

グラフは隣接リストを使用して表されるため、ダイクストラの最短パスアルゴリズムの複雑さはO（E log V）です。 。ここで、Eはエッジの数、Vは頂点の数です。

入力と出力

Input:
The adjacency list of the graph with the cost of each edge.

Output:
0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4

アルゴリズム

dijkstraShortestPath(g : Graph, dist, prev, start : node)

入力- グラフg、距離を格納するdistリスト、先行ノードのprevリスト、および開始頂点。​​

出力- 開始から他のすべての頂点までの最短経路。

Begin
   for all vertices u in (V - start) do
      dist[u] := ∞
      prev[u] := φ
   done

   set dist[start] = 0 and prev[start] := φ

   for all node u in V do
      insert u into queue ‘Q’.
   done

   while Q is not empty do
      u := minimum element from Queue
      delete u from Q
      insert u into set S

      for each node v adjacent with node u do
         if dist[u]+cost(v) < dist[v] then
            dist[v] := dist[u]+cost(v)
            prev[v] := u
      done
   done
End

例

#include<iostream>
#include<set>
#include<list>
#include<algorithm>
using namespace std;

typedef struct nodes {
   int dest;
   int cost;
}node;

class Graph {
   int n;
   list<node> *adjList;
   private:
      void showList(int src, list<node> lt) {
         list<node> :: iterator i;
         node tempNode;

         for(i = lt.begin(); i != lt.end(); i++) {
            tempNode = *i;
            cout << "(" << src << ")---("<<tempNode.dest << "|"<<tempNode.cost<<") ";
         }
         cout << endl;
      }
   public:
      Graph() {
         n = 0;
      }

      Graph(int nodeCount) {
         n = nodeCount;
         adjList = new list<node>[n];
      }

      void addEdge(int source, int dest, int cost) {
         node newNode;
         newNode.dest = dest;
         newNode.cost = cost;
         adjList[source].push_back(newNode);
      }

      void displayEdges() {
         for(int i = 0; i<n; i++) {
            list<node> tempList = adjList[i];
            showList(i, tempList);
         }
      }

      friend void dijkstra(Graph g, int *dist, int *prev, int start);
};

void dijkstra(Graph g, int *dist, int *prev, int start) {
   int n = g.n;

   for(int u = 0; u<n; u++) {
      dist[u] = 9999;   //set as infinity
      prev[u] = -1;    //undefined previous
   }

   dist[start] = 0;   //distance of start is 0
   set<int> S;       //create empty set S
   list<int> Q;

   for(int u = 0; u<n; u++) {
      Q.push_back(u);    //add each node into queue
   }

   while(!Q.empty()) {
      list<int> :: iterator i;
      i = min_element(Q.begin(), Q.end());
      int u = *i; //the minimum element from queue
      Q.remove(u);
      S.insert(u); //add u in the set
      list<node> :: iterator it;

      for(it = g.adjList[u].begin(); it != g.adjList[u].end();it++) {
         if((dist[u]+(it->cost)) < dist[it->dest]) { //relax (u,v)
            dist[it->dest] = (dist[u]+(it->cost));
            prev[it->dest] = u;
         }
      }
   }
}

main() {
   int n = 7;
   Graph g(n);
   int dist[n], prev[n];
   int start = 0;

   g.addEdge(0, 1, 3);
   g.addEdge(0, 2, 6);
   g.addEdge(1, 0, 3);
   g.addEdge(1, 2, 2);
   g.addEdge(1, 3, 1);
   g.addEdge(2, 1, 6);
   g.addEdge(2, 1, 2);
   g.addEdge(2, 3, 1);
   g.addEdge(2, 4, 4);

   g.addEdge(2, 5, 2);
   g.addEdge(3, 1, 1);
   g.addEdge(3, 2, 1);
   g.addEdge(3, 4, 2);
   g.addEdge(3, 6, 4);
   g.addEdge(4, 2, 4);
   g.addEdge(4, 3, 2);
   g.addEdge(4, 5, 2);
   g.addEdge(4, 6, 1);
   g.addEdge(5, 2, 2);
   g.addEdge(5, 4, 2);
   g.addEdge(5, 6, 1);
   g.addEdge(6, 3, 4);
   g.addEdge(6, 4, 1);
   g.addEdge(6, 5, 1);

   dijkstra(g, dist, prev, start);

   for(int i = 0; i<n; i++)
      if(i != start)
         cout<<start<<" to "<<i<<", Cost: "<<dist[i]<<" Previous: "<<prev[i]<<endl;
}

出力

0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4