C++で指定された範囲にあるBSTサブツリーをカウントします

入力として二分探索木が与えられます。目標は、開始と終了の範囲の間にノード値を持つBSTのサブツリーの数を見つけることです。 startが5で、endが50の場合。次に、すべてのノードの重みが5以上50未満のBSTのサブツリーをカウントします。

入力 −以下に示すツリー−範囲[3-6]

出力 −範囲内にある木の数− 2

説明 −ノード4および6の場合のみ。それらのサブツリー（NULL）は3〜6の間にあります。

入力 −以下に示すツリー：範囲[12-20]

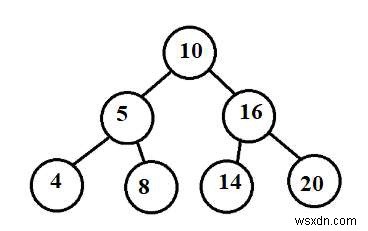
出力 −範囲内にある木の数− 3

説明 −ノード16、14、および20の場合。それらのサブツリーは12〜20の間にあります。

以下のプログラムで使用されているアプローチは次のとおりです

• 構造Btreenodeは、ツリーのノードを作成するために使用されます。情報部分は整数であり、サブツリーを指すための左右のポインターを自己参照します。

• 関数Btreenode*insert（int data）は、データをinfoとして、左右のポインターをNULLとしてノードを作成するために使用されます。

• 特定の構造に対して挿入関数を呼び出して、BSTを作成します。ルートノードに右からノードを追加するには（root-> right =insert（70）;）、ルートの左側にノードを追加します（root-> left =insert（30）;）。

• 変数lとhは、範囲の最小値と最大値を格納するために使用されます。

• 可変カウントは、lからhの範囲にあるツリー内のBSTのカウントを格納します。最初は0です。

• 関数getBtreeCount（Btreenode * root、int low、int high、int * count）は、BSTのルート、範囲の左右の境界、およびカウントのアドレスをパラメーターとして受け取り、各再帰呼び出しのカウントの値を更新します。

• 現在のルートについては、NULLかどうかを確認し、NULLの場合は、ツリーの一部ではないため1を返します。

• 現在のノードについては、その左右のサブツリーノードがすべて指定された範囲内にあるかどうかを確認します。再帰呼び出しによってgetBtreeCount（root-> left、low、high、count）; andgetBtreeCount（root-> right、low、high、count）;

• 両方のサブツリーが範囲内にあり、現在のノードも範囲内にある場合、現在のノードをルートとするツリーは範囲内にあります。インクリメントカウント。 if（left &&right &&root-> info> =low &&root-> info <=high）and ++ * count; 1を返します。

• 最後に、カウントはすべてのサブツリーのカウントとして更新された値になります。

• 結果をカウントで印刷します。

例

#include <bits/stdc++.h>
using namespace std;
// A BST node
struct Btreenode {
   int info;
   Btreenode *left, *right;
};
int getBtreeCount(Btreenode* root, int low, int high, int* count){
   // Base case
   if (root == NULL)
      return 1;
      int left = getBtreeCount(root->left, low, high, count);
      int right = getBtreeCount(root->right, low, high, count);
      if (left && right && root->info >= low && root->info <= high) {
         ++*count;
      return 1;
   }
   return 0;
}
Btreenode* insert(int data){
   Btreenode* temp = new Btreenode;
   temp->info = data;
   temp->left = temp->right = NULL;
   return (temp);
}
int main(){
      /* BST for input
         50
        / \
       30 70
      / \ / \
20 40 60 80 */
   Btreenode* root = insert(50);
   root->left = insert(30);
   root->right = insert(70);
   root->left->left = insert(20);
   root->left->right= insert(40);
   root->right->left = insert(60);
   root->right->right = insert(80);
   int l = 10;
   int h = 50;
   int count=0;
   getBtreeCount(root, l, h, &count);
   cout << "Count of subtrees lying in range: " <<count;
   return 0;
}

出力

Count of subtrees lying in range: 3