C++の配列に存在するキーKの確率

サイズ「n」の配列で与えられ、タスクは、配列で利用可能な場合、与えられた要素kの確率を見つけることです。

配列内の要素の数に等しい「n」まで配列全体をトラバースし、指定された要素またはキー「k」を検索します。要素がその確率を計算するよりも配列に存在する場合は、0を出力します。

入力

arr[] = { 1, 2, 3, 4, 5, 6}
K = 5

出力

probability of a key 5 in an array is :0.166

入力

arr[] = { 1,2,3,4,5,6,7 }
K = 8

出力

probability of a key 5 in an array is :0

説明

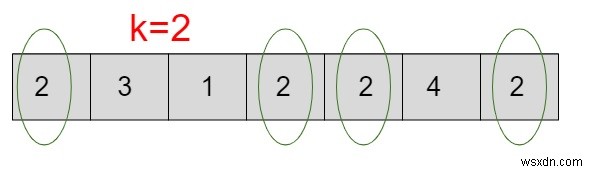
上記の配列はサイズ7とキー2の配列であるため、配列はキー値2を検索するために7回トラバースされます。2が識別されるたびに、一時変数を1ずつインクリメントし、要素が2以外の場合は次に移動します。カウンターをインクリメントせずに要素。最後に-

• カウンターが0の場合、これはキーが配列に存在しないことを意味し、確率は0になります

• カウンターが0以外の値である場合は、数式を適用してキー「’k’」の確率を計算します

  Probability（k）=「k」オカレンスの総数/要素の総数

  「K」発生の総数=4

  配列内の要素の総数=7

  key（k）の確率=4/7 =0.57

アルゴリズム

Start
Step 1→ declare function to calculate probability of key in an array
   float probab_key(int arr[], int size, int key)
      declare float count = 0
      Loop For int i = 0 and i < size and i++
      IF arr[i] = key
         Set count++
      End
   End
   return count / size
Step 2→ In main()
   Declare int arr[] = { 1, 2, 3, 4, 5, 6}
   Declare int key = 5
   Declare int size = sizeof(arr) / sizeof(arr[0])
   Call probab_key(arr, size, key)
Stop

例

#include <bits/stdc++.h>
using namespace std;
// calculate the probability of a key in an array
float probab_key(int arr[], int size, int key){
   float count = 0;
   for (int i = 0; i < size; i++){
      if (arr[i] == key)
         count++;
   }
   return count / size;
}
int main(){
   int arr[] = { 1, 2, 3, 4, 5, 6};
   int key = 5;
   int size = sizeof(arr) / sizeof(arr[0]);
   cout <<"probability of a key "<<key<<" in an array is :"<<probab_key(arr, size, key);
   return 0;
}

出力

上記のコードを実行すると、次の出力が生成されます-

probability of a key 5 in an array is :0.166667