RubyでBig-O表記を調べる
「そのためのBig-O表記は何ですか?」という質問を聞くことほど私を怖がらせなかった時期がありました。学校での話題を思い出しましたが、数学と関係があったので(これは私の最強の科目ではありませんでした)、それを黒く塗りつぶしました。
しかし、私のキャリアが進むにつれて、私は自分自身に気づきました:
- パフォーマンスチャートを見る
- 遅いクエリをデバッグしようとしています
- 負荷が増加した場合にコードがどのように保持されるかを検討したかどうかを尋ねられます
Big-Oを学ぶために戻って(わかりますか?)と決めたとき、私はその高レベルの単純さに驚いていました。この記事で学んだことを共有して、エンジニアの仲間がフライングカラーのインタビューに合格するだけでなく、パフォーマンスが高くスケーラブルなシステムを構築できるようにします。
私は約束します、Big-Oは見た目ほど怖くないです。一度理解すれば、プロファイリングツールを実行しなくても、アルゴリズムを調べてその効率を簡単に見分けることができます。
Big-O表記とは何ですか?
Big-O表記は、「ねえ、このアルゴリズムの最悪の場合のパフォーマンスは何ですか?」と言うための空想的な方法です。 O(n)またはO(1)として記述された関数を見たことがあるかもしれません。これは次のことを意味します:
- O(n) -最悪の場合の実行時間は、入力サイズ(n)が増加するにつれて直線的に増加します
- O(1) -最悪の場合の実行時間は、どのサイズの入力でも一定です
...そしてこれが何を意味するのかを本当に理解するには、漸近線について学ぶ必要があります
漸近線?
高校の代数に戻って、教科書をほこりを払い、限界と漸近線の章を開いてみましょう。
- 制限分析: ある値に近づくと関数がどうなるかを見る
- 漸近解析: f(x)が無限大に近づくと何が起こるかを見る
たとえば、関数f(x)=x ^ 2+4xをプロットするとします。
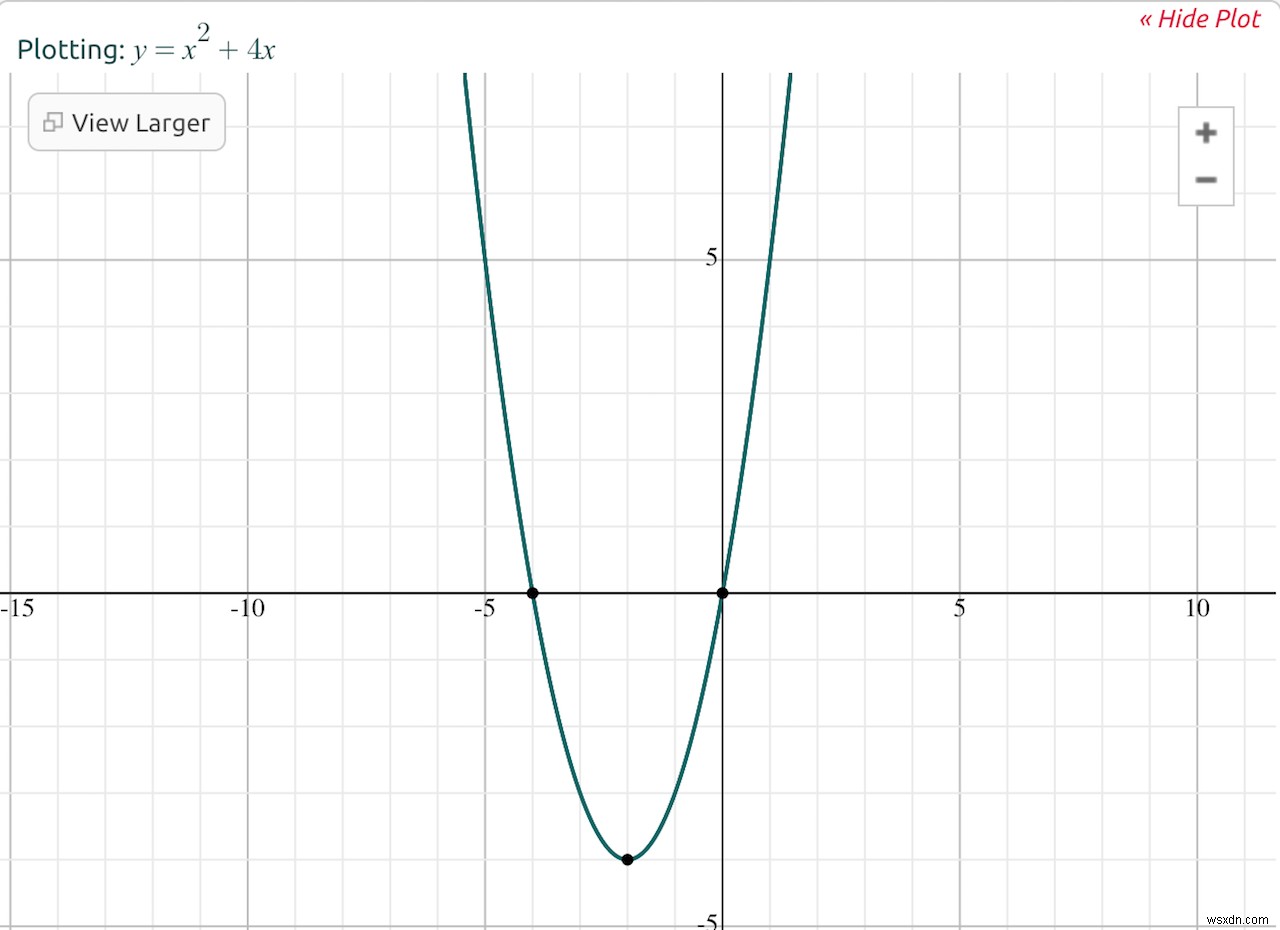
次の分析を実行できます。-制限分析: xが増加すると、f(x)は無限大に近づくため、xが無限大に近づくときのf(x)=x ^ 2+4xの限界は無限大であると言えます。 -漸近解析: xが非常に大きくなると、4x項はx^2項と比較して重要ではなくなります。したがって、xの値が無限大に近づくと、f(x)=x ^ 2 + 4xはf(x)=x^2とほぼ同等になると言えます。
関数の一部が「重要ではない」と言う方法を理解するために、元の関数に異なる数値を差し込んだときに何が起こるかを考えてみてください。たとえば、x =1の場合、関数は1 + 4(5に等しい)を返します。ただし、x =2,000の場合、関数は4,000,000 + 8,000(4,008,000に等しい)を返します。x^2項は4xよりも合計に大きく貢献しています。
Big-O表記は、入力のサイズが変化したときにアルゴリズムの実行時間がどのように変化するかを説明する1つの方法です。
アルゴリズムの実行時間を決定するものは何ですか?
干し草の山から針を見つけるのにどれくらいの時間がかかるかを尋ねると、干し草の山にどれだけの干し草があるのか知りたいと思うでしょう。 「10個」と答えれば、1、2分で針が見つかると確信していると思いますが、「1,000個」と言えば、それほど興奮しないでしょう。
知っておくべき情報がもう1つあります。追加された干し草の各部分のスタックを検索するのにどれくらい時間がかかりますか?そして、干し草の量が無限に近づくとどうなりますか?
これは、上記の漸近解析の例と非常によく似ています。私たち全員がこれを理解していることを確認するために、もう1つの例を見てみましょう。関数f(x)=5x ^ 2 + 100x+50を考えてみましょう。この関数の2つの部分を別々にプロットできます。
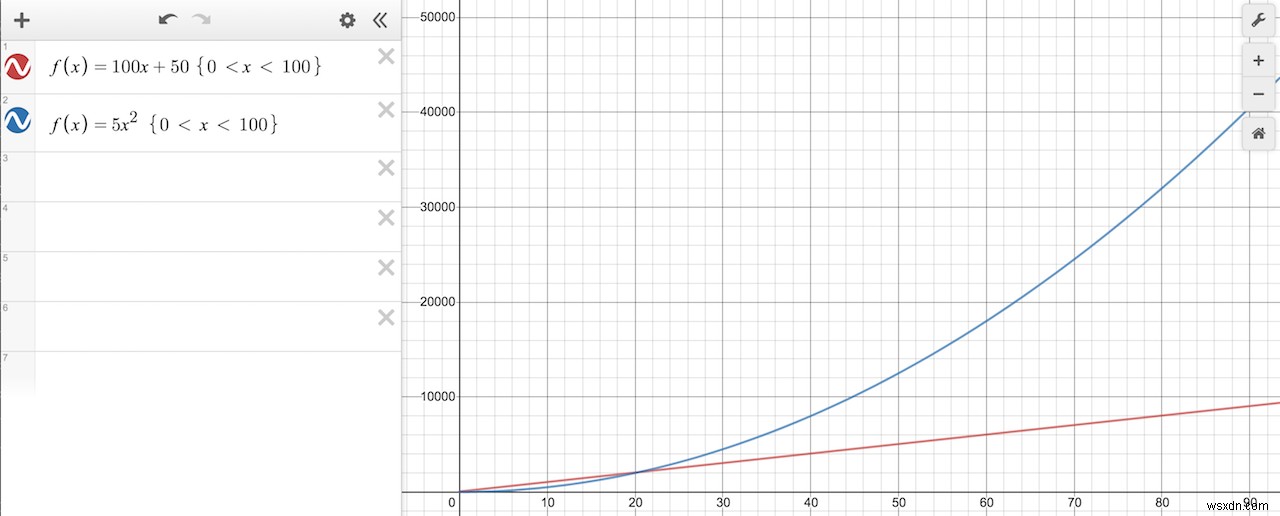
前の例と同様に、5x^2項は最終的に100x+50項よりも大きくなるため、それらを削除して、f(x)=5x ^ 2 + 100x+50の実行時間はx^2として増加すると言うことができます。
もちろん、プログラムを実行している実際のコンピューターの速度や使用されている言語など、実行時間に影響を与える他の要因があることにも言及する価値があります。
線形探索アルゴリズムのBig-O分析を行いましょう。線形検索はデータセットの先頭から始まり、ターゲット要素が見つかるまでトラバースします。
これがRubyでの実装です。
def find_number_via_linear_search(array, target)
counter = 0
# iterate through the given array starting
# at index 0 and continuing until the end
while counter < array.length
if array[counter] == target
# exit if target element found
return "linear search took: #{counter} iterations"
else
counter += 1
end
end
return "#{target} not found"
end
このメソッドに次のようなスピンを与えることができます:
# Let's create an array with 50 integers
# and then re-arrange the order to make
# things more interesting
array = [*1..50].shuffle
find_number_via_linear_search(array, 24)
これを数回実行したところ、次の結果が得られました。
=> "linear search took: 10 iterations"
=> "linear search took: 11 iterations"
=> "linear search took: 26 iterations"
関数のBig-O表記を分析するときは、最悪の場合のシーンリオ(別名:漸近線の上限)に注意します。
これを直感的に考えると、反復の最小数は1になります。これは、ターゲット要素が配列の0の位置にあるときに発生します。反復の最大数(または最悪の場合のシーンリオ)は50です。これは、ターゲット要素が配列に見つからなかった場合に発生します。
配列に100個の要素がある場合、最悪の場合は100回の反復になります。 200要素? 200回の反復。したがって、線形探索のBig-O表記は単純にO(n)です。ここで、nは要素の数です。
二分探索を使用したより複雑な例!
次に二分探索について考えてみましょう。 事前に並べ替えられたのバイナリ検索を行う方法は次のとおりです。 配列:1。真ん中の要素を取る
2. element == targetの場合 完了しました3。 element > targetの場合 配列の上半分を破棄します4。element < targetの場合 アレイの下半分を破棄します。5。残りのアレイで手順1からやり直します
注:Rubyistの場合は、このアルゴリズムを実装する組み込みのb-searchメソッドがあります。
たとえば、辞書があり、世界の「パイナップル」を探しているとします。辞書の真ん中のページに行きます。たまたま世界が「パイナップル」だったら、もう終わりです!
しかし、私の推測では、辞書の真ん中はまだ「p」に含まれていないので、「ラマ」という単語が見つかるかもしれません。文字「L」は「P」の前にあるので、辞書の下半分全体を破棄します。次に、残ったものでプロセスを繰り返します。
線形探索と同様に、二分探索の最良の実行時間は1回の反復です。しかし、最悪のケースは何ですか?これは16個の要素を持つ配列の例です-二分探索を使用して23という数字を見つけたいとしましょう:
[2, 3, 15, 18, 22, 23, 24, 50, 65, 66, 88, 90, 92, 95, 100, 200]
最初のステップは、インデックス7の数値である50を確認することです。50は23より大きいため、右側のすべてを破棄します。これで、配列は次のようになります。
[2, 3, 15, 18, 22, 23, 24, 50]
真ん中の要素は18になり、23未満なので、今回は下半分を破棄します。
[22, 23, 24, 50]
どちらになるか
[22, 23]
最終的に
になります[23]
合計で、16の長さの配列でターゲットにしている数を見つけるために、配列を半分に4回分割する必要がありました。
これを一般化すると、二分探索の最悪の場合のシーンリオは、配列を半分に分割できる最大回数に等しいと言えます。
数学では、対数を使用して、「この数を取得するために、この数のいくつを乗算しますか?」という質問に答えます。問題に対数を適用する方法は次のとおりです。
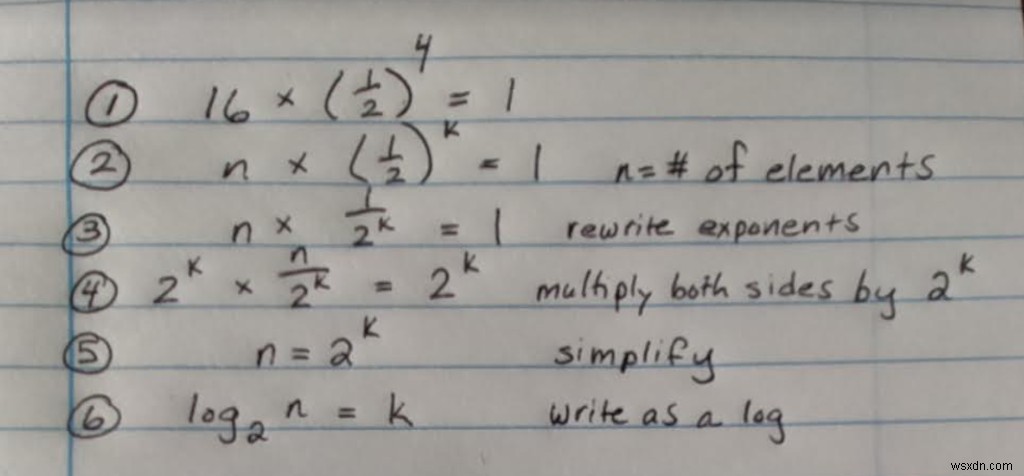
したがって、Big-O、つまりバイナリ検索の最悪の場合の実行時間はlog(base 2)nであると言えます。
Big-O表記は、「ねえ、これの最悪のケースは何ですか?」と言うための空想的な方法です。コンピュータサイエンスは別として、実際の例は、壊れた蛇口を修理するのにどれくらいの費用がかかるかを配管工に尋ねたときに何が起こるかということかもしれません。彼は、「まあ、それが2,000ドルを超えないことを保証することができます」と答えるかもしれません。これは上限ですが、あまり役に立ちません。
このため、他のBig-O表記がよく使用されます。たとえば、Big-Thetaは下限と上限の両方を考慮します。この場合、配管工は「まあ、1,000ドル以上になることはありませんが、2,000ドルを超えることはありません」と応答します。これははるかに便利です。
読んでいただきありがとうございます。この投稿が、Big-O表記を少なくとも少し怖くないトピックにするのに役立つことを願っています。
-
TCmallocを使用したRubyのメモリ割り当てのプロファイリング
Rubyではメモリ割り当てはどのように機能しますか? Rubyはページと呼ばれるチャンクでメモリを取得し、新しいオブジェクトはここに保存されます。 次に… これらのページがいっぱいになると、より多くのメモリが必要になります。 Rubyは、mallocを使用してオペレーティングシステムからより多くのメモリを要求します 機能。 このmalloc 関数はオペレーティングシステム自体の一部ですが、使用できる代替の実装があります。 それらの実装の1つは、Googleのtcmallocです。 TCmallocはGoogleパフォーマンスツールスイートの一部です。 これらのツールを使用し
-
Rubyでパーサーを構築する方法
構文解析は、一連の文字列を理解し、それらを理解できるものに変換する技術です。正規表現を使用することもできますが、必ずしもその仕事に適しているとは限りません。 たとえば、HTMLを正規表現で解析することはおそらく良い考えではないことは一般的な知識です。 Rubyには、この作業を実行できるnokogiriがありますが、独自のパーサーを作成することで多くのことを学ぶことができます。始めましょう! Rubyでの解析 パーサーの中核はStringScannerです クラス。 このクラスは、文字列のコピーと位置ポインタを保持します。ポインタを使用すると、特定のトークンを検索するために文字列をトラバ
